I'm trying to understand /simulate the communication between 2 smartphones by means of ultrasounds. As this is a general study I'm considering that the smartphones are equipped with the "typical" most common kind of transducers. One of them is broadcasting a sound and the other recording it. I would like to know under what conditions is the transmitted sound properly recorded. The first thing I did was trying to understand how directivity at this frequency affected the transmission. You can see that analysis here .
Now I'm trying to understand the technical parameters in the MEMS digital microphone and microspeaker (the kind of sound transducers most commonly used in smartphones). I'll assume that the transmitting smartphone is equipped with a speaker of this type and that the receiver is equipped with a microphone of this type.
In the speaker specification I can see :
Rated Input Power : 0.5W(2.0Vrms)
S.P.L : 83±3dB/0.1m/0.1W at 0.8,1.0,1.2,1.5KHz average
The speaker frequency response is:
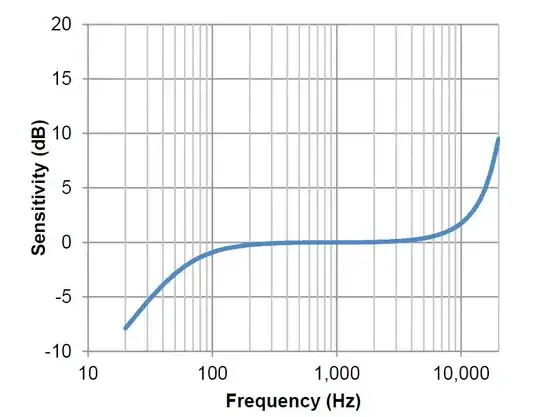
In the microphone specification I can see :
Sensitivity : 94 dB SPL at 1 kHz : -26 dBFS
The microphone frequency response is:
My questions are:
Is the sensitivity the difference between maximum acoustic signal (maximum SPL) at the mic input (which causes full-scale digital word, 16 bits? ) and the 94 dB SPL reference? So, if the mic sensitivity is –26 dBFS at 94 dBSPL, is maximum SPL 120 dBSPL? (–26 dBFS = 94 dBSPL – 120 dBSPL) Is it alright to mix dBFS and dBSPL ?
This is a PDM smartphone so it's output is only 1 bit. But if we assume that after proper conversion we obtain a 16 bit when the maximum acoustic signal (120 dBSPL) is being received, at 94 dBSPL will its output be about 11 bits?
Assuming that we are working at 1 kHz if the speaker generates 83±3 dBSPL at 10 cm and we place the microphone at this distance, how many useful bits will it output?
What can I do to find out the speaker generated SPL when it is supplied with 0.5W (instead of 0.1 W which is the only data given)?
What can I do to find out the speaker generated SPL and microphone sensitivity at, lets say, 18 kHz?
If mic SNR is 64.5 dB. How many useful bits above the noise floor can it work with?