23

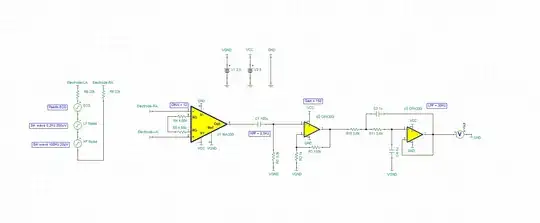
A discontinuity causes a signal to have infinite sinusoidal components, but a triangle wave is continuous, I was taking a class in which an instructor said that since the triangle wave is continuous it can be represented by a finite number of sine components and also showed a finite addition of multiple frequencies of sinusoids which did give the shape of a pure triangle wave.

The only problem I have in mind is that the derivative of a triangle wave is not continuous as it is a square wave and hence would need infinite sum of sinusoids so if one derivates the both sides of the formula of the Fourier series of a triangle wave, we would get a square wave being shown as a sum of finite number of sinusoids. Would that not be incorrect?

Peter Mortensen
  • 1,676
  • 3
  • 17
  • 23
Syed Mohammad Asjad
  • 447
  • 4
  • 12
  • 11
    The triangle wave does have an infinate fourier series .Remember that tutors are fallible . – Autistic Aug 11 '17 at 10:10
  • What did your instructor say when you asked him? – Solar Mike Aug 11 '17 at 10:12
  • @SolarMike I have not asked him yet, I will surerly now since it came up in my mind :) – Syed Mohammad Asjad Aug 11 '17 at 10:20
  • 6
    @Syed Mohammad Asjad: your reasoning with the derivative is correct. Maybe you have a better understanding of the matter than your instructor. – Curd Aug 11 '17 at 10:34
  • 6
    In fact, in order to have a finite Fourier series, the function *and ALL of its derivatives* must be continuous. All of the derivatives of a sinusoid are continuous, and this is also true of any finite sum of sinusoids. – Dave Tweed Aug 11 '17 at 11:12
  • It takes all of 10 seconds to check Wikipedia to confirm that a [triangle wave](https://en.wikipedia.org/wiki/Triangle_wave) has an infinite number of non-zero harmonics – Nayuki Aug 12 '17 at 02:11
  • 1
    Not an answer, but : Fourier series with finite coefficients are very restrictive. Most periodic functions have infinite Fourier series. However, the smoother the function, the more rapid the decay of the coefficients at infinity. If a function is k times differentiable with bounded derivative, then its Fourier coefficients (c_n) decay as fast as 1/n^(k + 1), as can be seen by induction. For analytic functions (functions with convergent Taylor series, ie. even smoother than infinitely differentiable), the decay is exponential. The triangle has Fourier series that is exactly 1/n^2. – Alexandre C. Aug 13 '17 at 13:31
  • @AlexandreC.: Can I get a clue? Normally a series with coefficients of 1/n^2 can be summed to a finite series but apparently this one can't. – Joshua Aug 13 '17 at 20:13
  • @Joshua, summing 1/n^2 is perfectly fine. Here you sum 1/n^2 times sin(nx). Now, sum(1/n^2 * sin(2pi nx)) converges to a triangle function. And even sum(1/n * sin(2pi nx)) converges to a rectangle function pointwise. – Alexandre C. Aug 13 '17 at 20:45

7 Answers7

22

a triangle wave is continuous

Quote from here: -

The triangle wave has no discontinuous jumps, but the slope changes discontinuously twice per cycle

Having the slope change discontinuously also means an infinite range of sinusoidal components.

For instance, if you time integrated a square wave you produce a triangle wave but, all the hamonics of the original square wave are still present after the time integration: -

enter image description here

Andy aka
  • 434,556
  • 28
  • 351
  • 777
22
instructor said that since the triangle wave is continuous it can be represented by a finite number of sine

You either didn't get this right or the instructor misspoke. It's not sufficient for the signal itself to be continuous, but all derivatives must be continuous too. If there is any discontinuity in any derivative, then the repeating signal will have a infinite series of harmonics.

A triangle is continuous, but its first derivative is a square wave, which is not continuous. A triangle wave therefore has a infinite series of harmonics.

Olin Lathrop
  • 310,974
  • 36
  • 428
  • 915
  • 1
    Nope did not mis hear, neither did he misspoke because he said it twice and also asked the class later what he had said, and exactly what i had thought :) – Syed Mohammad Asjad Aug 11 '17 at 12:14
  • @SyedMohammadAsjad you are both right. From google; *misspeak:* "express oneself in an insufficiently clear or accurate way." I think that one of you is using "insufficiently clear" and the other is using "insufficiently accurate". – uhoh Aug 12 '17 at 02:14
  • Although the wording of this answers somewhat suggest it, the fact that all derivatives exist (and hence are continuous, by the existence of the next derivative), is still far from sufficient for having a finite Fourier series. Most Fourier series for periodic signals, however smooth (class $\mathcal C^\infty$, or even analytic) have infinitely many nonzero components; it is hard to come up with a description of those that don't other than "finite sums of sines and cosines". All that smoothness implies is a with which coefficients _tend_ to 0. – Marc van Leeuwen Aug 13 '17 at 09:09
  • a brick filter can make the number of harmonics finite and it still looks /\/\/\/\/\/ trinagular with at least 20 , far from infinte – Tony Stewart EE75 Aug 16 '17 at 04:46
12

Math proof:

Take a function made up of the weighted sum of a finite series of sine/cosine components.

Its derivative is also a weighted sum of a finite series of sine/cosine components. Same if you derivate any number of times.

Since sine and cosine are continuous, the function and all its derivatives are continuous.

Thus, a function having a discontinuity in any of its derivatives can't be built with a finite series of sine/cosine components.

Kevin Reid
  • 7,444
  • 1
  • 25
  • 44
bobflux
  • 70,433
  • 3
  • 83
  • 203
  • Exactly what i had thought, thankyou :) – Syed Mohammad Asjad Aug 11 '17 at 12:13
  • Should be "sine and cosine are smooth" not just continuous--but the gist is correct, a finite sum of sines and cosines is smooth so can't have discontinuities in any of its derivatives – nimish Aug 11 '17 at 13:59
  • 1
    @nimish He proves that all derivatives are finite sums of (co)sines, therefore he only needs continuity of (co)sines, not smoothness :-) – yo' Aug 11 '17 at 20:25
  • Yep, missed that. Though from the analyticity of $\exp(z)$ for $z\in\mathbb{C}$, it follows trivially anyway. – nimish Aug 11 '17 at 23:24
  • Kudos for the math answer that *explains* the math instead of just pasting it! – uhoh Aug 12 '17 at 02:15
  • Yeah. I simply didn't know the word "smooth function" (in french it is written "infinitely derivable") – bobflux Aug 12 '17 at 07:49
8

Good answers abound here, but it really depends on your interpretation of "can be represented by".

One has to understand that a triangle wave is a theoretical mathematical construct that can not actually exist in reality.

Mathematically speaking, in order to get a pure triangle wave you would need an infinite number of harmonic sine-waves, but to get a representation of a triangle wave most of those components are too small to matter, get lost in the background noise of the system, or are of such high frequency to no longer be transmittable.

As such, in practice, you only require a finite number to get a usable representation. How good you want that representation dictates how many harmonics you need to use.

Trevor_G
  • 46,364
  • 8
  • 68
  • 151
  • 1
    That is indeed one of the things to look at, I'll surely ask my teacher if he meant that because you are right, in reality we do not go to the infinite frequencies at all, not even in the square wave (which isn't a pure square) :) – Syed Mohammad Asjad Aug 11 '17 at 16:15
  • While you're right that a triangular wave is a math construct, your reasoning is wrong. The fact that you can't make it of finitely many harmonics does not provide a proof that you can't make it at all. – yo' Aug 11 '17 at 20:26
  • @yo' indeed that is one of those things I think a lot of us have a hard time with. If a triangle wave = infinite number of sine waves at some point you cant add or pass the harmonics. If it's just a triangle wave.... generated by some other means... then what... how do you transmit it.. and how does the thing that is transmitting it know the difference... Gives me a headache thinking about it.. Basically, even if it's just a short piece of wire or PCB trace... it can't without distorting it. – Trevor_G Aug 11 '17 at 20:33
  • 1
    The difference between the mathematical ideal and the real world, in a nutshell. – peterG Aug 13 '17 at 14:59
4

Another approach.

Let's call x(t) the triangle wave and y(t) it's derivative, which is a square wave, hence discontinuous.

If x(t) were a finite sum of sinusoidal signals, its derivative, by the linearity of that operation, would be a finite sum of derivatives of sinusoidal signals, i.e. again a finite sum of sinusoidal signals.

But this latter signal cannot be the square wave y(t), because a finite sum of sinusoidal signals is continuous. Hence we have a contradiction.

Therefore x(t) must have infinite Fourier components.

LorenzoDonati4Ukraine-OnStrike
  • 24,350
  • 5
  • 62
  • 107
3

I propose a much simpler test to be used in practice. If the wave has any sharp corners it requires infinite sinusiodal components to build.

Why? Because a finite series of sinusiods cannot make a sharp corner. This is proven from induction on the decomposition rule of sums (that is, Σ (a + b) = Σ a + Σ b for all finite summations and all unconditionally convergent infinite summations).

Joshua
  • 287
  • 1
  • 6
2

The set of functions that are expressible by a finite Fourier series are:

$$F:=\{f(x)=a_0+\sum_{n}^{n \in N}(a_n\cos{nx}+b_n\sin{nx})\}$$

For all finite sets of indices N. Term-by-term differentiation shows that the derivative is (1) continuous and (2) also in F. Since the derivative of the triangle wave is not continuous, the function of the triangle wave is not in F.

This proof is based off of discontinuity, but most continuous functions also do not belong to F. Since no polynomial or exponential function can be expressed as a finite sum of sines and cosines, the only members of F are those written out explicitly in the form above.

Jared Goguen
  • 121
  • 4