This question is related to a question asked earlier regarding a linear power supply build. It turns out that the circuit is oscillating quite badly; an issue not uncommon in feedback circuits. I've been researching compensation techniques in order to cure the problem and, as an introduction, I've found this tutorial series to be very helpful.
It doesn't deal with my situation exactly (which is to be expected) but (thanks to its intuitive approach), I've been able to create a simulation model in spice that attempts to help me understand the open loop frequency response, which is also as the text explains, the loop gain Ab when the closed loop gain is unity.
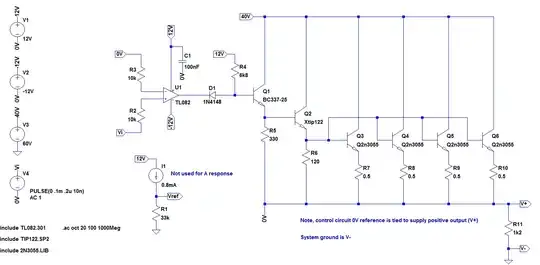
The original Farnell power supply on which this circuit is based can be found here and you can see from the spice model image below that I haven't changed much from the original.
In order to find the OL response, I've removed any negative feedback (including the original local compensation) and tied the inverting input to control ground (0V). Then running the AC analysis, I get the following:
If I understand the result correctly, the response across the entire frequency domain is attenuated. If this is true and I'm doing this correctly, how can this circuit ever really oscillate? Since according to the tutorial mentioned above, the circuit is unstable (at unity gain) when the gain at f(-180 degrees) is greater than 1.
UPDATE:
Fix suggested by Andy, some local feedback to equalize the inputs (but not enough to affect the response at FOI):