I understand that, in order for an op-amp to function correctly, a DC feedback loop from the output to either the inverting or the non-inverting input (depending on the external circuitry) is required.
What is the purpose of DC feedback when using op-amps? Why is it necessary and what would the effects be without it?
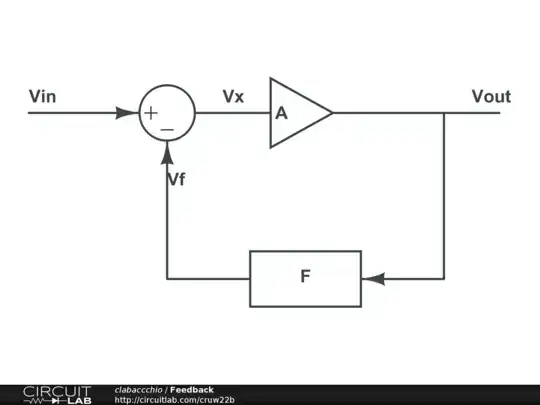
You already know that an opamp has very high open-loop amplification, typically 100 000 times. Let's look at the most simple feedback situation:
The opamp will amplify the difference between \$V_+\$ and \$V_-\$:
\$ V_{OUT} = 100 000 \times (V_+ - V_-) \$
Now \$V_+ = V_{IN}\$ and \$V- = V_{OUT}\$, then
\$ V_{OUT} = 100 000 \times (V_{IN} - V_{OUT}) \$
or, rearranging:
\$ V_{OUT} = \dfrac{100 000}{100 000 + 1} \times V_{IN}\$
That's as good as
\$ V_{OUT} = V_{IN}\$
This is a voltage follower, a \$\times\$1 amplifier, which is mostly used to get a high input impedance and a low output impedance.
The feedback reduces the very high open-loop amplification to \$\times\$1. Note that the high amplification is needed to get \$ V_{OUT}\$ as close as possible to \$V_{IN}\$.
edit
Now by using just a fraction of the output voltage in the feedback we can control the amplification.
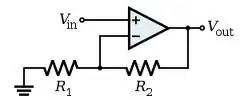
Again
\$ V_{OUT} = 100 000 \times (V_+ - V_-) \$,
but now \$V_+ = V_{IN}\$ and \$V- = \dfrac{R1}{R1+R2} \times V_{OUT}\$, then
\$ V_{OUT} = 100 000 \times (V_{IN} - \dfrac{R1}{R1+R2} \times V_{OUT}) \$
Or:
\$ V_{OUT} = \dfrac{100000 \times V_{IN}}{\dfrac{R1}{R1+R2} \times 100000 + 1} \$
The term "1" can be ignored, so that
\$ V_{OUT} = \dfrac{R1+R2}{R1} \times V_{IN} \$
Notice that in both the voltage follower and this non-inverting amplifier the actual amplification factor of the opamp cancels provided it is high enough (>> 1).
An ideal opamp has infinite gain. It amplifies the difference in voltage between the + and - pins. Of course in reality this gain is not infinite, but still quite large.
The output of the opamp (at to some extents the input also) is constrained by the power supply, we can't get out more than the supply puts in.
If we simply put signals into the opamp without feedback it would multiply them by infinity and get a binary output (it would saturate at the supply rails)
So, we need some way of controlling the gain. That is what the feedback does.
The feedback (DC as well as AC) takes part of the amplified output from the input, such that the gain is constrained much more by the feedback network, which is predictable, and much less by the massive (and unpredictable) open loop gain.
Even in an AC only circuit we still need feedback that works at DC (zero Hz) or the gain would be only that of the open loop for DC signals. You AC signal though constrained would be swamped by the DC open loop gain.
The ideal op-amp has infinite gain, and this is of little use in analog electronics. The feedback is used to limit the gain of the circuit. You can find many examples in the wiki article.
Consider the simple feedback loop:
\$ Vout = A \cdot Vx \$
\$ Vf = F \cdot Vout \$
\$ Vx = Vin - Vf = Vin - FVout \$
\$ Vout = A \cdot Vin - A \cdot F \cdot Vout \$
\$ Av = \frac{Vout}{Vin} = \frac{A}{1+AF} \$
In the case of the op-amp, its gain defines A: it will be a quite nasty function, because these amplifier are made for just giving brutal gain, and won't have a nice linear function. Luckily, if you look at Av, if A is big enough it will cancel the 1 and itself leaving 1/F to determine the gain.
In the case of the non-inverting amplifier, the block F is a voltage divider, so it will be something like 1/X. This will set the gain of the amplifier to X.
In the case of real op-amps, A won't be infinite, but big enough to allow cancelling it in the DC gain equation. And the advantages of feedback are even more, like increasing bandwith, linearity, S/N ratio and more. For instance, in a closed loop the gain is determined only by the inverse of the feedback gain, provided that the op-amp gain is big enough.
Actually, one resistor only is not that useful as a feedback, as it behaves the same as a short circuit. A voltage divider to ground makes it behave like a fixed ratio multiplier of the same factor (for the same reason mentioned above).
The purpose of DC feedback is to define what you want the op-amp to do, i.e. what its output voltage will be. Without it, the output will rise or fall until it hits the power rails.
This can be useful, and there is a large market for op-amps specialized to work this way, called "comparators".
A comparator is simple: if the + input is greater than the - input, the output is +Vcc. Otherwise, the output is −Vee. The schematic symbol is the same as an op-amp, and they can even with sufficient effort be coaxed into working in both roles, but in practice, the two types are highly specialized, and such efforts are not really worth it.
With the DC feedback path, an op-amp can be stable at some point other than "output hard against the rails", and the circuit is generally designed to find that point.
Rather than thinking about it statically, think about an op-amp as an integrator. Whenever its + input is greater than its − input, an op-amp's output will RISE, rapidly. This rise should being the inputs closer together, finally stopping when they are equal. Likewise, + input less than − input will cause the output to fall. The feedback is generally to the − input because that's the simplest way to make a circuit that works this way.
A typical power supply error amplifier has no DC feedback path:
I can assure you, however, that this amplifier works quite well.
Visualize this error amplifier controlling a buck converter. Vcomp would be used to control the duty cycle of a switch, which controls current flow through an inductor and controls Vout. As Vcomp increases, so does the duty cycle, which causes Vout to increase and Vcomp to decrease. The compensation network will increase or decrease Vcomp in a controlled manner, to force Vout to match Vref (as closely as the opamp will allow).
[ Of course, the power train is providing some semblance of DC feedback, but I digress :) ]
DC feedback in op-amp uses due to stability, also op-amp gain is too high so we use feedback to have a specific gain in output
