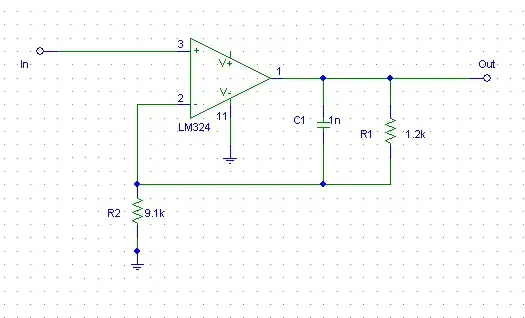
The thing is to rewrite your original equation in a well-ordered form, following a low-entropy format, this is the key to unveil the various quality factors \$Q\$ and the resonant frequencies \$\omega_0\$. A second-order polynomial form obeys the following expression when the terms \$a_0\$ and \$b_0\$ are different than 0 and factored as a leading term:
\$H(s)=H_0\frac{1+\frac{s}{Q_N\omega_{0N}}+\left(\frac{s}{\omega_{0N}}\right)^2}{1+\frac{s}{Q_D\omega_{0D}}+\left(\frac{s}{\omega_{0D}}\right)^2}\$ in which \$H_0=\frac{a_0}{b_0}\$, \$Q_D=\frac{\sqrt{b_2}}{b_1}\$ and \$\omega_{0D}=\frac{1}{\sqrt{b_2}}\$. Substitute the terms \$a_1\$ and \$a_2\$ for the numerator quality factor and resonant frequency.
Now your expression is \$\frac{s^2+0.02s+1001}{(s^2+2s+101)(s^2+20s+10100)}\$. However, from the Bode plot, you have a dc gain of -120 dB, a double zero in the numerator which creates a notch at the resonant frequency of 1 rad/s then followed by 4 resonating poles located at 10 and 100 rad/s. Start by factoring 1001 in the numerator \$N(s)\$. You should find \$N(s)=1001(1+\frac{0.02}{1001}s+\left(\frac{s}{1001}\right)^2)\$. Now proceed with the denominator \$D(s)\$ by factoring 101 and 10100. You should get: \$D(s)=101\times10100(1+\frac{0.02}{101}s+(\frac{s}{101})^2)(1+\frac{20}{10100}s+(\frac{s}{10100})^2)\$
From these expressions, you should extract the dc gain \$H_0=\frac{1001}{101\times10100}=981\times10^{-6}\$ or -60 dB. So you already see that this value does not match the dc gain from the Bode plot. Looks like a 60-dB attenuation is missing. Determine the \$Q\$s and the resonant frequencies with the given formulas and then plot the result to see how it matches your chart:
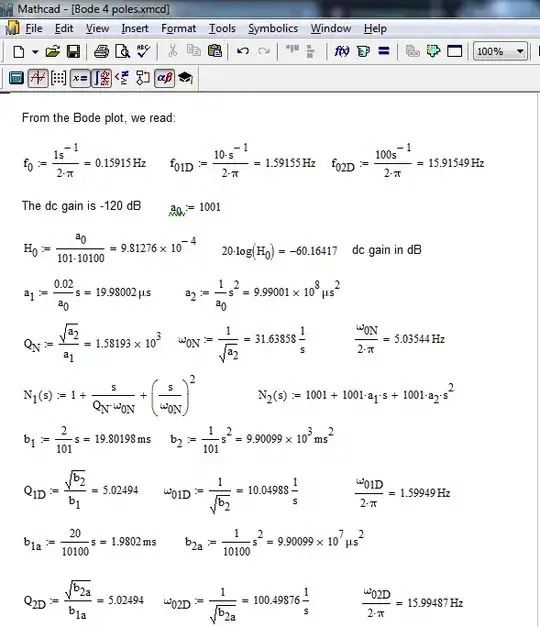
Then plot the polynomial forms and the raw-expression:
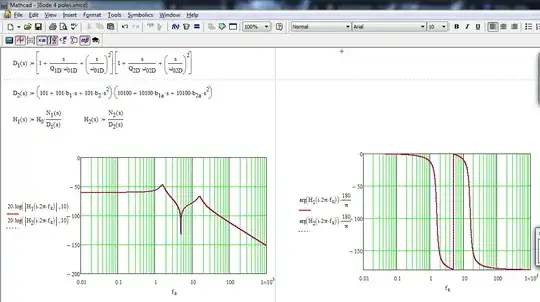
As expected, the dc gain is wrong, the notch is misplaced but the poles seem to be ok (the \$x\$-axis in in Hz and not in rad/s). So it seems, at first look, that the problem lies in the numerator while the denominator looks ok. Considering the missing 60-dB attenuation (a ratio of 1000), I have updated the dc gain to \$H_0=\frac{1.001}{101\times10100}=9.8\times10^{-7}\$ which is -120 dB. I can now divide all terms in the numerator by 1001 and plot the newly-resulting Bode plot:

The horizontal scale is now in rad/s and the final result does not look bad : )
So the correct high-entropy expression is given below, please note the correct dimensions of the various coefficients to keep a unitless transfer function:
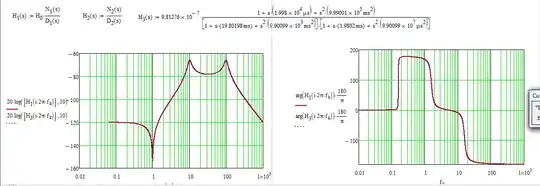
You have the values of the various \$Q\$s and resonant frequencies in the Mathcad shots. The damping ratio \$\zeta\$ and \$Q\$ are linked by \$\zeta=\frac{1}{2Q}\$. You will learn more about low-entropy expressions and Fast Analytical Circuits Techniques (FACTs) here.
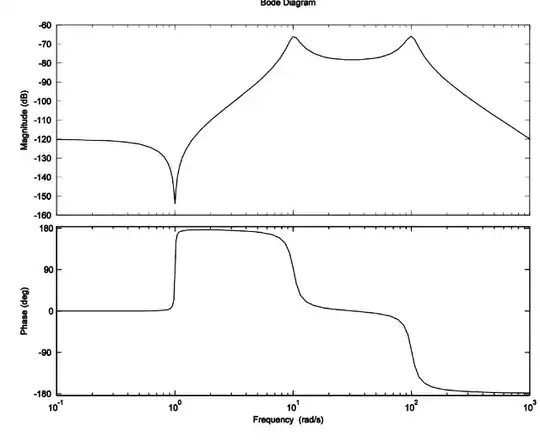 The solution manual says the function plotted is $$\frac{s^2+0.02s+1001}{s^2+2s+101)(s^2+20s+10100)}$$ What I know is the Bode plot for $$\frac{s^2+2ζω_ns+ω_n^2}{ω_n^2}$$ and the inverse of that.
The solution manual says the function plotted is $$\frac{s^2+0.02s+1001}{s^2+2s+101)(s^2+20s+10100)}$$ What I know is the Bode plot for $$\frac{s^2+2ζω_ns+ω_n^2}{ω_n^2}$$ and the inverse of that.