I have come across the Salcone-Bond paper Selecting Film Bus Link Capacitors For High Performance Inverter Applications (PDF), which shows equations for single-phase inverters. But I can't seem to find any guide or paper on how to size DC link capacitors for 3-phase PWM controlled inverters.
How can I size the DC link capacitor of a 3 phase inverter?
If the inverter is required to supply an inductive load, the DC link capacitor needs to be sized to carry the reactive component of the load. The reactive load current will produce a high ripple current in the link capacitor. That will require a higher link capacitance than would be required to smooth the ripple voltage of the rectifier. Look for papers or a text on PWM variable frequency drive (VFD) design.
The diagram below shows the basic power circuit for rectifier-inverter or AC to AC converter with a DC link. The load is shown as single motor as for a VFD, probably the most common use of this circuit.
For an inductive load, the load current lags the inverter output voltage. That causes current to flow through the inverse parallel diodes back to the DC link during a part of each cycle. The inverter load consists of real power, mostly converted to mechanical output power, and reactive volt-amperes required to maintain the magnetic fields. The real power is seen at the DC input I(InvDC) as the average DC current multiplied by the average DC voltage. The reactive volt-amperes are seen at the same point as a ripple current component. Since reactive energy can not pass through the rectifier, it is seen as ripple current in the DC link capacitor. The DC link capacitor must, in effect, act as a power factor correction capacitor for the motor.
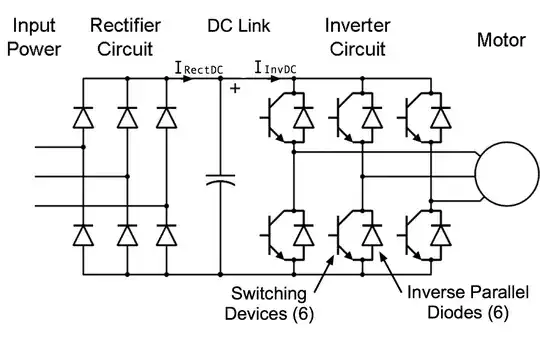
DC-Link capacitor for DC-filtering and energy buffering. Targets power electronics devices for renewable energy systems, battery charging systems, motor drives and power supplies. Source: Vishay.
I never heard the term before and had to look it up. I take it to mean the reservoir capacitor on the DC bus.
If your inverter has a three-phase power supply then you will not need much capacitance as one phase is always "up".
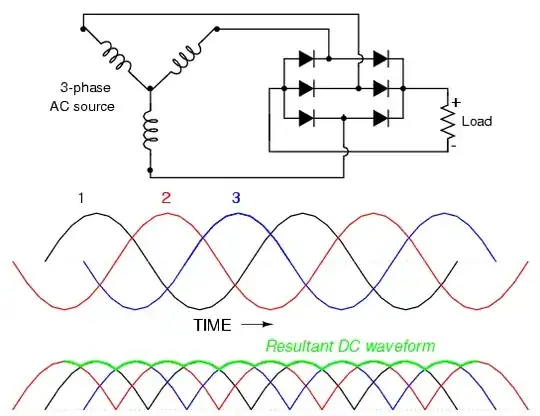
Figure 1. With a three-phase supply the DC has a low ripple value without any capacitor smoothing.
For a single-phase supply we need to keep the voltages up when the instantaneous AC voltage drops during phase reversal. Calculating the capacitor value shouldn't be any different than any other power supply.
Determine what the maximum voltage droop your inverter can tolerate at maximum load current.
On a 50 Hz supply the capacitor will be charged every 10 ms. Between charge pulses the capacitor voltage droop will be given by
$$ \Delta V = \frac {It}{C} $$
Where \$ \Delta V \$ is the voltage droop, I the current in amps, t the time in seconds, and C the capacitance.
Example: DC bus = 200 V, 180 V minimum. DC current = 2 A.
$$ C = \frac {It}{V} = \frac {2 \times 0.01}{20} = 1\;mF $$
Explanation of formula:
Charge on a capacitor is given by \$ Q = CV \$. Current is defined as the charge passing a point per second - \$ I = \frac {dQ}{dt} = C \frac {dV}{dt}\$. If we approximate and assume that the current is linear (rather than an exponential delay) for the period of interest then \$ dV = I \frac {dt}{C} \$.
Generally speaking the capacitors need to be big enough to keep the voltage ripple on the DC bus below some specified level. Beyond that there may be some EMC concerns regarding current (AC). The limiting factors here are heat (ESR losses) and hence lifetime of capacitors (can be very difficult to estimate due to lack of manufacturers data).
One main issue is, that a 1 phase AC load draws an oscillating power at 2x base frequency and this has to be supplied by the DC link capacitors if you want to avoid huge ripple currents, whereas a balanced 3-phase AC load draws a constant power and so you don't have that problem. This is one reason why 3-phase PV inverters are preferred to 1-phase. The ripple current in the 3 phase is at the PWM switching frequency as the DC link must supply the motor current during the transistor"on"time during each switching state of the inverter, and this is a quare wave current which at a max at 50% duty cycle.
Have fun.
