As most folk know, \$s=\sigma+j\omega\$ (where \$j\omega\$ is the frequency along the x-axis in a bode plot or spectrum analysis). However, in a bode plot, \$\sigma\$ has no apparent meaning but it is actually the "unseen" z-axis (in and out of the screen/page).
If the natural resonant frequency of the RLC circuit were 1 radian per second then the z-axis is purely zeta, the damping ratio. That's the simple answer. The fuller pictures (hopefully) should be apparent with this image showing example bode plots along the top and the pole zero diagram in 3D at left bottom: -
As you should be able to see, the "z-axis" (or \$\sigma\$ axis) has values corresponding to \$\omega_n\$ (the natural resonant frequency aka \$\frac{1}{\sqrt{LC}}\$) and the damping ratio zeta (\$\zeta\$).
s is supposed to be sigma + jw, and sigma arises so that the transform
integral converges. However, when constructing bode plots, this is
completely ignored. Why?
Hopefully you can see that now.
Is there a physical meaning to sigma?
Basically it's damping ratio multiplied by natural resonant frequency for values of zeta between 0 and 1.
The effects on the bode plot of zeroes and poles are to change the
slope in 20dB incrementals (bode magnitude), the gain isn't really
infinite on the poles, since s is replaced by jw and if the poles are
real, s being complex will never have those real values so that the
bode plot goes infinite. What is the meaning of this?
The gain IS infinite on the poles, indisputably. The rest of that particular question is probably irrelevant due to that misconception.
A region of convergence (ROC) for s can be found, which is a range of
values for s so that the integrals converge. What is the ROC useful
for? What happens when the frequency is outisde the ROC? Textbooks are
pretty good in showing how to find these ROCs, but not in making clear
what effects they have in your circuit.
I have no idea what this means or how to answer it, sorry.
the transfer function 1/(s+1) has a pole at s = -1. This means that
sigma = -1 and omega is zero. However, when make Bode plot, s is set
to be equal to jomega that is pure imaginary number. So the transfer
function at s = jomega is not infinity at all. If it is not infinity
then what value it would be also why are we interested in s = j*omega
instead of s = -1 for the function above?
Think like this - you have a table and on that table you stand your pencil upright in the middle (this is the pole). You then place a really thin and pliable handkerchief over the end of the pencil. The contour made by the handkerchief produces a tent effect but more perfect: -
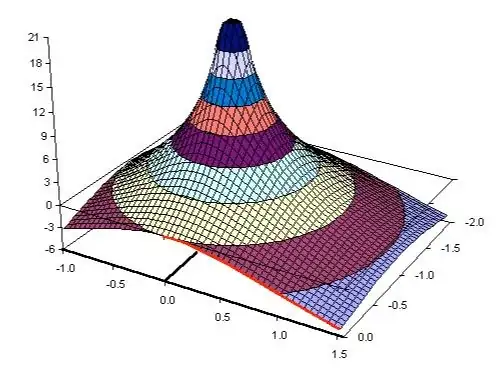
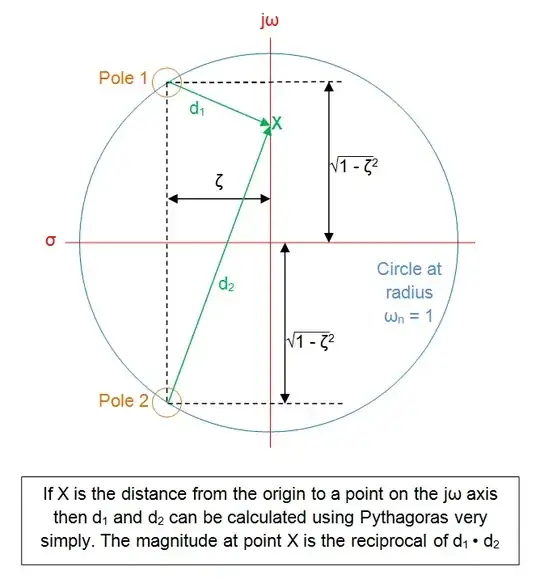
At any point from that pole position, the handkerchief has a numerical value that is perfectly defined. For instance, if you draw a circle around the pole, all points on the handkerchief would have the same amplitude. If the pole is at -1 then, the amplitude when s = 0+j0 (the origin) is 1. The amplitude at 0+j1 needs a little more thought - the distance from the pole to 0+j1 is 1.4142 therefore the amplitude is the reciprocal of 1.4142 i.e. 0.7071 (aka the 3 dB point of the simple RC filter your numbers numerical example describes).
At 0+j2, the distance from the pole is \$\sqrt{1^2+2^2}\$ = 2.236 and the amplitude is therefore 0.4472.
At 0+j10 (ten times the 3 dB frequency), the distance is \$\sqrt{1^2+10^2}\$ = 10.05 and the amplitude is 0.0995.
This can be extended to complex pole pairs and zeroes too. At any point on the jw axis (called X below) the amplitude is: -