Conjugate, non-conjugate and single poles in an RLC circuit system

Question

In all the texts I encountered so far, I find the following pole-zero diagram example for an RLC series circuit:

The transfer function for the above circuit can be found as:

H(s) = XC/(R + XL + XC) = (1/sC)/[R + sL + (1/sC)]

H(s) = 1/(LCs² + RCs + 1)

---

But when I plot the pole-zero diagram of the above circuit for different R,L and C values, I don't always obtain the poles as conjugate.

Below are three different pole-zero diagram of the above RLC circuit for different R,L and C values:

1-) Conjugate Poles

R = 10;

C = 0.00001;

L = 0.001;

2-) Non-conjugate poles

R = 10;

C = 0.001;

L = 0.001;

3-) Pole at the origin

R = 100;

C = 0.001;

L = 0.001;

Question:

What can we say about the real response of the circuit for each three case above by considering the locations of the poles? In other words, what does it mean poles being conjugate, being asymmetric/non-conjugate and being at the origin only for an RLC series circuit? (Especially, in the second case there is two different non-conjugate poles which is the most confusing situation to say something about the system)

Edit:

Following the answer I was able to reveal the higher pole for the third case:

Answer 1

The circuit you have drawn, the \$RLC\$ network, does not feature zeros, only poles. Should you add a small resistance in series with the capacitor, then you would add a zero. The equation you have derived shows a second-order polynomial form in the denominator: \$D(s)=1+b_1s+b_2s^2\$. It can be advantageously factored in a canonical form such as \$D(s)=1+\frac{s}{Q\omega_0}+(\frac{s}{\omega_0})^2\$ in which \$Q=\frac{\sqrt{b_2}}{b_1}\$ and \$\omega_0=\frac{1}{\sqrt{b_2}}\$. By quick identification with your expression, you can determine these values easily. Now, if you try to determine the roots of \$D(s)=0\$, or the poles of the transfer function, you end up with a pair of roots defined by \$s_{p1},s_{p2}=\frac{\omega_0}{2Q}(\pm\sqrt{1-4Q^2}-1)\$.

From this expression, you can see that depending on the value of \$Q\$, the expression under the square root can be positive or negative. If positive, the roots are real (there is no imaginary part) and the transient response is non-oscillatory. This is the case for a \$Q\le0.5\$. For a very low \$Q\lt\lt1\$, we can apply the so-called low-\$Q\$ approximation in which you consider the poles well spread apart. There is one in the low frequency domain (the root in your diagram is close to the vertical axis) while the second is in higher frequencies. You thus write \$D(s)\approx(1+\frac{s}{\omega_p1})(1+\frac{s}{\omega_p2})\$ in which \$\omega_{p1}=Q\omega_0\$ and \$\omega_{p2}=\frac{\omega_0}{Q}\$. It simply means that for a high value of the series resistance, the circuit can be replaced by two (isolated) cascaded \$RC\$ networked tuned at \$\omega_{p1}\$ and \$\omega_{p2}\$. If you drive your circuit with a step voltage, the output voltage is very sluggish without overshoot.

When \$Q=0.5\$, the roots are still real but coincident. The response is still non-oscillatory and \$D(s)\approx(1+\frac{s}{\omega_0})^2\$. If you drive your circuit with a step voltage, the output voltage rises quickly without overshoot.

Now if you reduce the series resistance further, \$Q\$ exceeds 0.5 and the roots involve imaginary notation: they become imaginary conjugates like one root located at -1+2j and the other at -1-2j for instance. Please note that the real part in these expressions is negative implying that in your \$s\$-plane diagram, the little "crosses" are in the left half-plane (LHP). We call them LHP poles or LHPP. The negative real parts model the losses in your circuit, the power dissipation that will damp oscillations and force the time-domain response to converge to a steady-state value as \$t\$ approaches infinity. If you drive your circuit with a step voltage, the output voltage rises quickly and overshoots.

As these losses become less and less (the circuit gains in efficiency), \$Q\$ increases - more pronounced overshoot in \$v_{out}(t)\$ - until the poles become pure imaginaries: the real parts are gone and the poles are located on the vertical axis. Should you excite the circuit with a transient pulse, the response would be oscillatory with sustained oscillations when the excitation is gone.

A pole at the origin is a different story. Having a pole at the origin simply means that your transfer function hosts a division by \$s\$: \$H(s)=\frac{1}{s(1+\frac{s}{\omega_p})}\$ features a LHP pole and a pole at the origin because \$D(s)=0\$ for \$s=0\$. Should you divide by \$s^2\$ instead, you have two poles at the origin etc. You have a pole at the origin in systems featuring an integrator for instance. The pole at the origin implies a gain approaching infinity in dc (when \$s=0\$), actually the op amp open-loop gain, which ensures a very low static error in the variable you control.

Answer 2

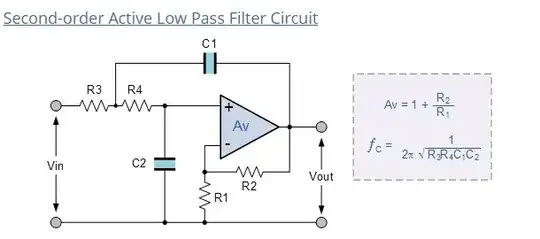
This general form for this type of low pass filter is: -

\$H(s) = \dfrac{\omega_n^2}{s^2 + 2\zeta \omega_n s+\omega_n^2}\$

And if you solve the quadratic in the denominator (to reveal the poles) you get: -

\$s = \dfrac{-2\zeta\omega_n \pm 2\omega_n\sqrt{\zeta^2-1}}{2}\$ \$ = \omega_n(-\zeta \pm \sqrt{\zeta^2-1})\$

Then, if you analyse the square root, you can see that for low damping (low zeta) you get the square root of a negative number hence that part of the equation involves "j" and you get conjugate complex poles at some fraction of +/-\$\omega_n\$.

When the damping (zeta) reaches unity, there are no more complex poles and a single pole lies on the real axis at \$-\zeta\omega_n\$. This then splits into two poles (along the real axis) as zeta rises above 1.

A low value of zeta is under-damped hence you get a peaky response in the bode plot and you get conjugate poles. When zeta = 1 you get critical damping and when zeta is greater than 1 you get a rather sloppy 2nd order filter that starts to look like a 1st order filter as R dominates over \$X_L\$.

To get numbers we need to know how zeta and omega relate to R, L and C values: -

\$\zeta = \dfrac{R}{2}\sqrt{\dfrac{C}{L}}\$ and \$\omega_n = \dfrac{1}{\sqrt{LC}}\$

---

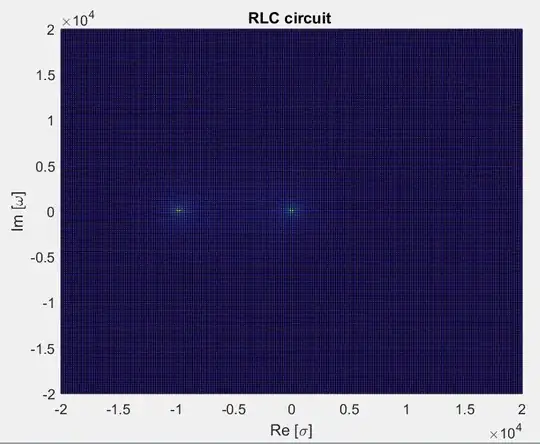
For R = 10, C = 0.00001 and L = 0.001, zeta = 0.5 and Wn = 10,000 and this is as you display the conjugate poles on your first graph.

---

For R = 10 and C = L = 0.001, zeta = 5 and Wn = 1,000 so the poles are at: -

\$s=1000(-5\pm\sqrt{24}\$) = -9899 and -101 and I can't precisely say if this corresponds with your graph but it looks close.

---

For R = 100 and C - L = 0.001, zeta = 50 and Wn = 1,000 so the poles are at: -

\$s=1000(-50\pm\sqrt{2499}\$) = -99,990 and -0.01 so you are not able to see the higher pole on your graph but otherwise I would say I get about the same result.

---

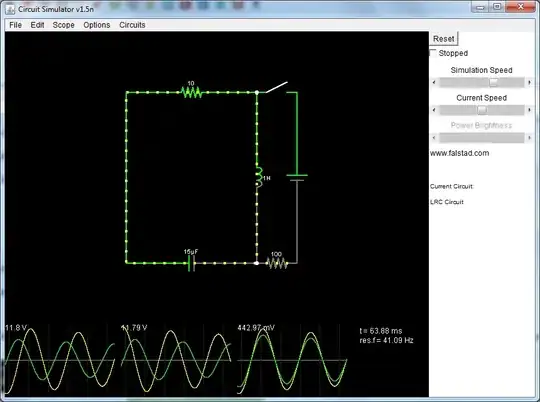
To substantiate the theory a bit more, this picture may be useful: -

It's also noteworthy that when both poles lie on the real axis (i.e. the over-damped situation), pole positions are: -

\$ = \omega_n(-\zeta + \sqrt{\zeta^2-1})\$ and \$ = \omega_n(-\zeta - \sqrt{\zeta^2-1})\$

And, if you did the math you would find that one pole is the normal conjugate of the other with respect to \$\omega_n\$ i.e. if one is ten times \$\omega_n\$ then the other is one-tenth of \$\omega_n\$.

In other words \$ = \omega_n(-\zeta + \sqrt{\zeta^2-1})\$ is the inverse of \$ = \omega_n(-\zeta - \sqrt{\zeta^2-1})\$.