Should I use resistors for LED

Question

Hi all,

This might be possibly the silliest question you have come across, but its bugging me out. Recently i have bought a 1Watt LED and when enquired with the vendor, he informed that the allowed max voltage is 3V.

So I was thinking that if I source three LED's in series from a 9V battery as shown in the above figure. Here the power source 9V is equal to the voltage dropped by LED's. So my question is

• Do i really need to use a current limiting resistor for LED's in the above circuit?
• Is it safe to use this circuit without resistors?

Thanks in advance.

P.S: Apologies if it was too silly.

Answer 1

You should always have a way of defining the current through an LED.

I prefer to call the resistors "current defining" rather than "current limiting" - current limiting sounds as if it is just a protection mechanism.

The resistors are there to set the desired current level. Without them the current will depend upon the particular LEDs, the battery level and temperature.

To just use a resistor to set the current level you need to provide a certain amount of excess voltage.

A 9v battery only provides 9v when it is new (actually it may be slightly more than 9v) but as it runs down the voltage will drop. An alkaline battery is not rundown until it reaches 0.9v per cell, for a 9v battery with 6 cells this is only 5.4v - if you put 3 LEDs in series they would probably dim appreciably when the battery was only 10% discharged.

You could probably use 2 LEDs in series that would have maximum voltage of 6v and then use a resistor to drop the remaining 3v.

For example if you use a 30ohm resistor it would cause about 100mA to flow when the battery was new that would drop to a few 10's of mA as the battery discharged.

If by 9v battery you mean the normal 9v battery they are not designed for such currents and are not a very good source of power for this application. At low currents they can provide about 500mAh but at 100mA they will probably provide less than half of that.

A resistor drops the voltage by throwing away the energy as heat, an electronic controller is more efficient and will get better life from the battery.

Answer 2

You always have to use a resistor with LED. It's mandatory in order to fix the current flowing through them. A diode needs a certain amount of current to work, you can provide this current thanks to a resistor and a very simple formula coming from Ohm's law (that you may know)

Is it safe to not add a resistor in this circuit?

Well, In my experience I never fry a diode but doing so but it's not recommended at all.

• The resistor is used to control the current through a diode. If there is no resistor, the current can potentially be very high.
• The resistor can drop the extra voltage. In your example, the voltage source fits exactly diode's need, but it's not always the case.

Answer 3

he informed that the allowed max voltage is 3V.

Don't listen to your vendor. To determine the configuration of your LEDs, you need to determine the forward voltage drop for each one. This typically depends on the color of the LED, and can be found in the datasheet. It can range from 0.5V all the way to 3V.

Let's assume that your vendor was referring to the voltage drop (check the datasheet!), powering it from a 9V battery in series would be a poor configuation. Firstly, a batteries voltage goes down with usage, for 9V as low as 5.4V as mentioned by some of the other answers. Secondly, the forward voltage of LEDs, have some variability and the total forward voltage of your 3 LEDs might be greater than 9V and will never turn on. Your options are either to use a different configuration (i.e. parallel) or have a greater voltage source.

To determine the resistor needed for your circuit you need to again look at your LED's datasheet, where it says it's constant current rating. For your LED based on the 1W description I will assume that it can handle up to:

$$ P = VI $$ $$ 1W = 3V \times I $$ $$I = 1W/3V = 333mA$$

To determine your resistor value, take your voltage source VCC, subtract the total voltage drop and devide by your current. For example if you had your 9V source, one 3V LED and you wanted 100mA:

$$V = IR$$ $$R = \frac{V}{I}$$ $$R = \frac{Vcc - V_{forward voltage}}{I}$$ $$R = \frac{9V - 3V}{100mA}$$ $$R = 60\Omega$$

and as a bonus, if you mess around with that last equation, and determine the current if R =0, you see there will be infinite current (not quite in reality) which shows why you should never hook up an LED without some sort of current limiting device.

Answer 4

• Do i really need to use a current limiting resistor for LED's in the above circuit?

Yes you need a current limiting resistor. As many answers have suggested, you should get hold of the datasheet of the LED. By observing the Forward Voltage vs Forward Current and Forward Voltage vs Luminous Intensity graphs you can determine the best combination of voltage and current for your circuit. Based on this, a suitable resistor value can be calculated.

• Is it safe to use this circuit without resistors?

No. Adding a resistor gives you control over the current flow and ensures the LED's don't go past their max ratings as specified in the datasheet. Not adding resistor might cause degradation in LED's efficiency and eventually lifetime.

Answer 5

The current through an LED is always defined ...by the impedances in the circuit (it is NEVER undefined or tending to infinite). Whether you have or need a series resistor will depend on the LED knee voltage, internal resistance and the power source.
When using LED's you typically want any added series resistor to be as low a value as possible to reduce power loss. You can test the LEDs using a variable power supply and there is no real problem testing without any external added series resistor.

To understand the LED you have to understand (at least to some degree) the characteristic model for the LED. While this is quite complex you can make huge simplifications and still end up with a quite effective way to analyze the circuit. The simplest DC model for a diode or LED is a voltage source, ideal diode (LED in this case) and resistor in series (the resistance is essentially the bulk resistance of the silicon).

With what you already know; that you have a diode with a Vf of 3 V and a power of 1 Watt, you can establish that you will need an If of 333 mA (P=V*I).

While we have no idea what the LED is that you have we could select a device for which there is a datasheet as an example.
Here's a datasheet for an LED selected from Digikey that will work continuously at a 1 watt level.

The Voltage current curve for this LED is as follows:

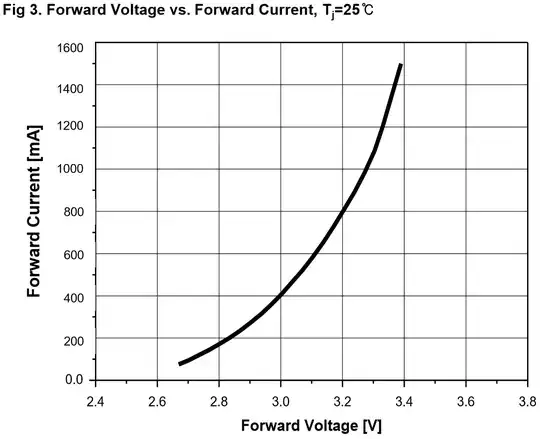From the curve above you can see that at 3 v the current (at 25 degC) is about 400 mA so for this LED that represents a DC power of about 1.2 W.

You can now make some piecewise linear approximations using the graph to find the LED knee voltage (the offset voltage) and the equivalent series resistance of this LED.

These approximations show that the LED probably has a knee (when it starts to conduct at significant levels) at about 2.5 -2.55 V and its series resistance is approximately 0.7 Ohm.

Armed with these numbers (and for this particular LED) you can see that 3 devices in series look like a 3*(2.55) offset voltage and about 2.1 Ohms series resistor.

For a well regulated 9 V supply the current flow without any addition series resistor would be approximately (9 - 7.65) / 2.1 --> 640 mA, and we can see from our piecewise approximation that this will be more than an actual LED string would pass from the actual datasheet LED curve. This gives enough information for a more focused design.

Let's imagine we need to design a torch with three of these LED devices in it with a maximum DC consumption of approximately 1 W per device (3 W total DC disipation). There are a couple of options available.

Option 1 - 9 V battery

The torch is battery powered with 6 * C cell batteries and you expect brand new batteries to be at (6 * 1.55 V from the datasheet) approximately 9.3 V, and at end of life they'd be about 7.65 V (3 * 2.55 V) and approaching zero current.

If the total power dissipation of the torch is 3 W, then the current from a 9.3 V source would be 325 mA.

If we consider the offset voltage fixed the total series R required is:

(9.3 - 7.65) / 0.325 = 5.2 Ohm

Since we have approximately 2.1 Ohms in the LEDs themselves we need to add an external resistor of:

(5.3 - 2.1) = 3.1 Ohms

This external resistor will dissipate (0.325^2 * 3.1) = 0.33 W
This would subtract from our target 3 W leaving you with 2.6 W DC consumption by the three LEDs in series.

Option 2 - 3 V battery

In this case if you were to configure the 3 LEDs in parallel we only need a 3 V supply.

A new battery (still the C cells, but organized as 2 in series and 3 pairs in parallel is (2 * 1.55 V) = 3.1 V

Each LED consists of the ideal LED plus a 0.7 Ohm series resistor so the current demand from the battery is now (3 * 0.325) = 970 mA.

If we consider the offset voltage fixed the total series R required is:

(3.1 - 2.55) / 0.970 = 0.57 Ohm

Since we have approximately (0.7 / 3) Ohms in the LEDs themselves we need to add an external resistor of:

(0.57 - 0.23) = 0.34 Ohms
This external resistor will dissipate (0.970^2 * 0.34) = 0.32 W

This is marginally less loss than that in the 9 V scenario, with an LED DC power of 2.68 W.

So either option (3 or 9 V) would appear to be effective for this type of use.

If you can't find a datasheet with I/V curves for your LED, then you can measure the knee voltage at some minimal current (say 5-10 mA) and Vf at a higher current that gives you your 1 W dissipation. Once you have these two points you have enough information to do a piecewise linear model and work out your resistance values.

Answer 6

So voltage and current both go hand in hand within a circuit. As you said, let's assume that LED's require forward volt bias of 3 V, you would need voltage greater than at least 10 V in order for the current to flow. Also, the voltage source should be able to provide at least 330 mA of current since these are 1 W LED (\$3~V \cdot 330~mA = 1~W\$). 330 mA is the max that the LED can withstand.

As far as I know, 330 mA is too much for a LED. Generally it's around 50 mA. Now consider you have a 12 V/1 A supply (quite commonly available) then you need to put a resistor so that it limits current to 330 mA and drops 3 V across itself (so that 9V is left for the 3 LED's). So by Ohm's law you need at least 9 Ohm (don't use those 0.25 W resistors, use 1 W resistor only) resistor in series for equal brightness.

I suggest you use 33 Ohm resistor and reduce the resistance based on the brightness you want.