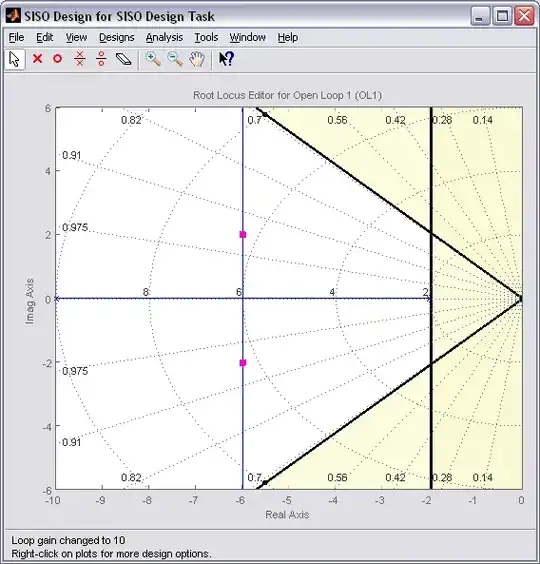
I am trying to design a P controller (proportional constant only) to satisfy certain overshoot and settling time requirements for my plant. My values for \$\zeta\$ and \$w_n\$ which would satisfy the requirements are 0.86 and 0.52 respectively. So I went ahead and made a root locus of the plant's transfer function showing the lines for \$\zeta\$ and \$w_n\$ using the sgrid command. This would help me find the value of K.
As seen in the plot, the root locus does not lie within the desired location (in between the two dotted lines and outside the semi-circle). I am not sure how I can select the desired pole locations in this case. I might be doing something wrong, or not fully understanding what needs to be done. Could someone please guide me here?
EDIT:
My plant transfer function is \$\frac{8.25}{6.6s^2+s}\$
I need a proportional controller for my plant which would meet my requirements of \$<0.5\%\$ overshoot and \$<8s\$ settling time