4

I'm reviewing nodal analysis on sinusoidal steady state circuits which my textbook typically only does mesh analysis on and I can't seem to get to the answer they obtained for an example problem.

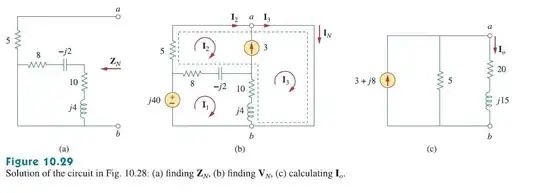
enter image description here

They obtain this after mesh analysis. enter image description here

My thought is that the middle node and top node are my only essential node but I assume that I'm treating it wrong since I'm not obtain the same solution.

Does anyone have any insight here?

This is simply for practice and my own knowledge.

Edit:

I obtained:

$$Io = 1.11897\angle19.5104°$$

The book obtained:

$$Io = 1.465\angle38.48°$$

Community
  • 1
jake mckenzie
  • 155
  • 6
  • What did you obtain? What are you expected to obtain? – jonk Jun 03 '17 at 20:39
  • I modified the post. I would include all the work the book did but but apparently I need at least 10 reputation to post more than two links and pictures count as links. – jake mckenzie Jun 03 '17 at 21:07
  • Thanks. I'll post something up (unless someone beats me to it with a better job of it.) – jonk Jun 03 '17 at 21:21
  • 1
    I am really lost somewhere. Your book is going through the longest and most difficult way to get Norton's equivalent. Instead of finding short circuit current \$I_\text{N}\$ you better workout open circuit voltage which, thru branch Vgen, R5 ohm and Igen, is simply \$\text{j}40\,\text{V}+5\,\Omega\times 3\,\text{A}\$ and then divide by \$Z_\text{N}\$ – carloc Jun 04 '17 at 05:45
  • The book always does examples like these with mesh analysis and I always mess up the mesh analysis. I know as an engineer I'll need to have proficiency with all skills but for these circuits in particular I have a hard time seeing where I need to start with them. – jake mckenzie Jun 05 '17 at 04:43

1 Answers1

2

I assigned \$V_A\$ to your \$a\$ node. I mentally grounded your \$b\$ node. Given that preface, nodal provides:

$$\begin{align*} \frac{V_A}{5\:\Omega}+\frac{V_A}{20\:\Omega+j 15\:\Omega}&=3\:\textrm{A}+\frac{j40\:\textrm{V}}{5\:\Omega} \end{align*}$$

(There's no need to worry about the "middle node" voltage because it is on the other side of a current source or else you have to go past a voltage source to get there. Either way, it doesn't matter.)

I used \$j40\:\textrm{V}\$ for your voltage source because it's \$90^\circ\$ out of phase and this is achieved by simply multiplying by \$j\$. The current source is \$0^\circ\$ so a simple \$3\:\textrm{A}\$ is fine.

Solve for \$V_A\$:

$$V_A=\frac{3\:\textrm{A}+\frac{j40\:\textrm{V}}{5\:\Omega}}{\frac{1}{5\:\Omega}+\frac{1}{20\:\Omega+j 15\:\Omega}}$$

And then you know that:

$$\begin{align*} I_0&=\frac{V_A}{20\:\Omega+j15\:\Omega}\\\\ &=V_A\cdot\frac{1}{20\:\Omega+j15\:\Omega}\\\\ &=\frac{3\:\textrm{A}+\frac{j40\:\textrm{V}}{5\:\Omega}}{\frac{1}{5\:\Omega}+\frac{1}{20\:\Omega+j 15\:\Omega}}\cdot\frac{1}{20\:\Omega+j15\:\Omega}\\\\ &=\frac{3\:\textrm{A}+\frac{j40\:\textrm{V}}{5\:\Omega}}{\frac{20\:\Omega+j15\:\Omega}{5\:\Omega}+1}\\\\ &=\frac{15\:\textrm{V}+j40\:\textrm{V}}{25\:\Omega+j15\:\Omega}\\\\ &\approx 1.14705882 + j0.911764706\\\\&\approx 1.46528455 \angle 38.4801982^\circ \end{align*}$$

Rounded, the above matches the answer you are supposed to get.

jonk
  • 77,059
  • 6
  • 73
  • 185
  • That was actually the equation I came up with too, but I guess I was inconsistent with how I set up my middle node which caused Va to come out differently. Thank you. I would vote you up if I could. – jake mckenzie Jun 04 '17 at 03:55
  • @jakemckenzie I did include the equation for your middle node, earlier. But removed it from my answer as it had no impact on the \$a\$ node. So it really doesn't matter what voltage is there, as it is cordoned off from your node \$a\$. Don't worry about the upvote. It's not why I'm here. You already paid me simply by letting me know that it helped. Thanks. Hehe. Since you are short on points, I'll add what I can to help you next time. – jonk Jun 04 '17 at 04:02