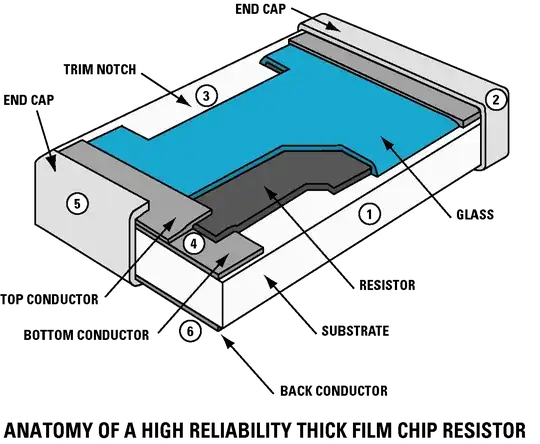
I'll try to simplify this for you... Hopefully successfully.
If you imagine making a resistor just by cutting pieces of a material, let's say a special metallic film;
You want your resistor to fit in a usable box, else it's pointless, so you cannot make super long strips or incredibly short ones. So you use film that's different thickness of the same metal.
Now, say that you have a bunch of thicknesses, each thickness is ten times less resistive than the one that's one step thinner. And they all have to be 10mm long to fit your box, so that you can only cut away from a standard strip width, let's say 5mm.
If you want to make 10 Mohm, you take the thinnest one, and you have to remove half of its width. So you have to remove 2.5mm. If the material works linearly, which we'll assume for the ease of it, that means you "cut away" 10 Mohm in 2.5mm. To remove 10 Ohm more or less, that would mean cutting with an accuracy of (brackets for clarity of order, not because they are needed):
(10 / 10000000) * 2.5mm = 2.5nm.
2.5nm is smaller than what we can do in silicon chip technology.
Written in meters that is 0.0000000025m, where for the uninitiated, one meter is close to one yard, or about the size of a long stride of an adult human.
If you wanted to get the same 10 Ohm error on a 100 Ohm resistor, you'd take the foil that's five steps up, which if it's still linear would get you about 50 Ohm (2 bits of 100 Ohm in parallel), so you'd have to cut off 2.5mm again. But this time, you can cut away only accurate to:
(10 / 100) * 2.5mm = 0.25mm.
That's something a practised person could do with a pair of scissors.
See the difference in difficulty there? Scissors versus can't even do it in microchips?
And that's when your resistor's box is allowed to be 10mm x 5mm, which is around 10 times the size of the most commonly used types these days.
Now, obviously resistors aren't made in an elf workshop full of reels of metal film... anymore... We've gotten much better at making more different thicknesses of different materials, so it's gotten better.
But, it does illustrate the point, even if you would use laser-trimming on everything, trimming to one part per million, which is 10 Ohm on 10 Mohm, is going to be a very difficult process to get consistent and it will even then still create a lot of parts that are over or under trimmed.
By accepting that any process in engineering is governed by statistics and percentages, as well as rules of average, we can very easily cope with resistors that are 10%, or 1% or 0.1% accurate, so there is no need to do it better for most cases.
Only when you need a very accurate reference, which is uncommon if your name isn't Fluke, Keysight, Keithley or any of those others, will you want someone to give you a resistor that's better than 0.001% and those are usually large ceramic plates with very accurately applied layers of resistive material, which then get cut to a very accurate recipe and will cost ridiculous amounts of money, even now. Though the 0.01% are finally getting close to affordable.