Calculate the thevenin resistance with diagonal resistors

Question

The question is:

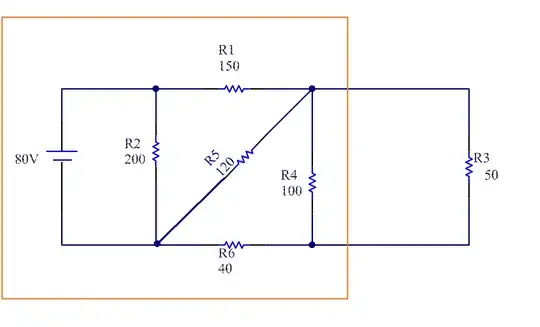
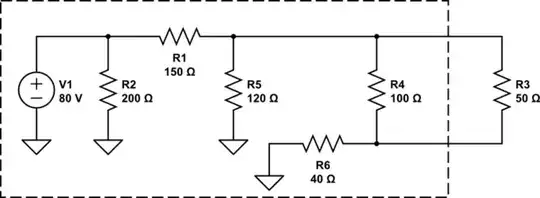
Replace the circuit with a Thevenin Equivalent Circuit and find the Thevenin Resistance (Rt) in ohms and find the current in R3.

I've used Thevenin before and solved quite a few equivalent circuits as well.

I've tried to redrawing the circuit, but I getting very confused on you would exactly go about combining these resistors. I found this exercise in a book, however, at the end of the book, it only shows the answer and not the approach. So the thevenin resistance should be 51.61 ohms.

You need to do the Thevenin’s theorem in the orange box.

So my first try was to consider R4 and R6 in series, then in parallel with R5, then in series with R1 to finish in parallel with R2. But obviously, that wasn't the right way to do it.

try searching harder https://electronics.stackexchange.com/questions/131604/thevenin-equivalent-resistance-of-circuit-with-diagonal-resistors?rq=1 — Tony Stewart EE75, May 12 '17 at 06:50
\$R_2\$ can be ignored. It sits across the voltage supply and cannot impact anything \$R_3\$ sees. Start there and redraw the schematic. — jonk, May 12 '17 at 07:06
"my first try was to consider R4 and R6 in series, then..." You are doing it backwards. You should be looking for the resistance as seen from the load R3, not as seen from the 80V generator. Short the generator and then redraw your circuit without R3. You want to find the resistance seen from what were R3's terminals. — Sredni Vashtar, May 12 '17 at 08:28
As @Mike said, what's wrong with Thevenin's theorem - determine the open circuit voltage and short circuit current and divide to find \$R_{TH}\$? It's a straightforward analysis. — Chu, May 12 '17 at 12:41
I know that a straightforward analysis, usally I don't have difficulty to solve problems with the Thevenin's theorem, but not for this problem, this is why I'm asking for help. @jonk I've try like you said, and it still doesn't work, maybe I am doing something wrong. — Liquidox, May 12 '17 at 16:09
@Liquidox There are dozens of ways of proceeding and I don't know which of them you want from me. But I can provide one, anyway. If you want it done differently I may, or may not, decide to go that way. (It's not fun being told "no, that's not what I wanted, I wanted it done using .") — jonk, May 12 '17 at 16:47
@Liquidox, once you short the voltage source, R2 is shorted too. So you proceed with R1//R5, then series with R6, then parallel with R4. The value you find is the 51.6 ohm resistance given in the solution. What is it that you don't understand? — Sredni Vashtar, May 12 '17 at 17:28
@Sredni Vashtar I understand now, I was just really confused... sorry for the trouble, I guess. — Liquidox, May 12 '17 at 17:33
@Chu it's just easier for me to use source transformations in this case. It's just a combination of some parallel and series resistors so you don't really have to write anything down. — Mike, May 12 '17 at 21:42

score 1 · Answer 1 · answered May 12 '17 at 17:08

1

Try the following sequence of steps. If you don't follow any of them, let me know:

schematic

^{simulate this circuit – Schematic created using CircuitLab}

schematic

^{simulate this circuit}

schematic

^{simulate this circuit}

schematic

^{simulate this circuit}

schematic

^{simulate this circuit}

schematic

^{simulate this circuit}

Done.

answered May 12 '17 at 17:08

jonk

77,059
6
73
185

@Liquidox Hopefully, you see it. \$V_{TH}\approx 17.2\:\textrm{V}\$ and \$R_{TH}\approx 51.6\:\Omega\$. – jonk May 12 '17 at 17:18

Sergiy Kolodyazhnyy · Answer 2 · 2017-05-12T17:52:41.553

The method here is fairly straightforward: ask what would be the resistance looking into the circuit from the load point of view, if the voltage source was replaced by a short ?

Imagine placing an ohm-meter at the terminals of R4. That turns out to look like R4 || ( R6 + ( R5|| R1 ) ). Question then is, where did R2 go ? Well, if you remember, we shorted out the voltage source, thus shorting out R2 as well.

If you go through calculations, that's:

R5 || R1 = (150*120)/(150+120) = 66.67 Ohm
R6 + ( R5|| R1 ) = 40 + 66.67 = 106.67 Ohm
R4 || ( R6 + ( R5|| R1 ) ) = (106.67*100)/(106.67+100) = 51.61 Ohm

score 0 · Answer 3 · answered Jul 19 '17 at 20:46

I'm not doing the work for you but just list two different ways to solve this:

You can apply Y→\$\Delta\$ transformation (or \$\Delta\$→Y transformation) and transform the circuit step by step into its Thevenin Equivalent or
you can use the standard approach for finding the Thevenin (or Norton) Equivalent (together with one of the general circuit analysis methods, i.e. Nodal or Mesh Analysis):
- find short circuit current \$i_{sc}\$ (i.e. replace R3 by short and find current through that connection)
- find open circuit volatge \$v_{oc}\$ (i.e. remove R3 and find voltage across the two nodes R3 was connected to)
- \$v_{th} = v_{oc}\$, \$R_{th}=\frac{v_{oc}}{i_{sc}}\$

Calculate the thevenin resistance with diagonal resistors

3 Answers3