Voltage reference that can drive current in both ways

Question

I am designing a device that at some point needs an oscillator in order to work. The whole circuit is fed by a 9 V battery. The V20 label corresponds to 20 V coming from a Boost converter whose input is the 9 V from the battery, and its output is 20 V.

The oscillator I'm looking forward to use can be seen in the picture below:

In the terminal with the label V10, I need a good reference of 10 V. I first thought of connecting the battery directly to it (9 V would not be so terrible), but the problem is that I realized that current can't flow both ways through a battery and, in this design, current should be able to do so.

In a nutshell, I need to put a reference of ~10 V in that terminal in such a way that current can flow in both ways in that branch. Also, it would be great if the solution was as simple as it can be (i.e. small amount of components). Is there a way to achieve this?

Answer 1

You can base your design in this question and its answers. In short, replace the resistor R22 by two resistors of equal value 1K, one of them connected to 0v, the other one connected to 20v.

(if, in other circuit elements you need also the virtual ground, this reference explains several methods to create one).

The circuit is:

^{simulate this circuit – Schematic created using CircuitLab}

Analysis:

\$V_o\$ will we a rectangular wave (ideal op amp), with low level 0v and high level \$V_{cc}\$ . If we analyze the voltage at \$V_+\$ we have:

^{simulate this circuit}

that means:

$$ 0 = \frac{V_{cc}-V_+}{R_4}+\frac{V_o-V_+}{R_2}+\frac{0-V_+}{R_3} = \\ V_{cc}/R_4+V_o/R_2-V_+(1/R_2+1/R_3+1/R_4) $$ Let \$V_H\$ the value of \$V_+\$ when \$V_o\$ is at its high level \$V_{cc}\$. Define \$V_L\$ the value of \$V_+\$ when \$V_o\$ is at its low level 0v:

$$ V_H = V_{cc} ~ \frac{1/R_2+1/R_4}{1/R_2+1/R_3+1/R_4}\\ V_L = V_{cc} ~ \frac{1/R_4}{1/R_2+1/R_3+1/R_4} $$

Now, the analysis of \$V_-\$.

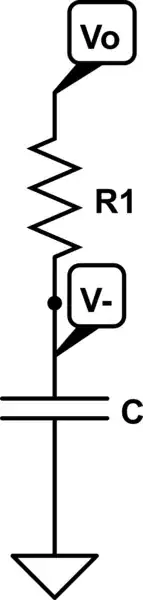
^{simulate this circuit}

When \$V_{cc}\$ jumps from low to high, \$V_-\$ goes from \$V_L\$ to \$V_H\$, charging C across \$R_1\$ from \$V_o=V_{cc}\$ and reaching the high level in a time \$T_H\$; when \$V_{cc}\$ is at low level, it goes from \$V_H\$ to \$V_L\$. The equations are (see at end of this explanation for the demonstration of the exponential).

$$ V_-(t) ~ = ~ (V_{cc}-V_L)~(1~ -~ e^{- t / R_1 C})+V_L \\ \frac{V_H-V_L}{V_{cc}-V_L} = 1 - e^{ - T_H / R_1 C} $$

thus

$$ T_H = - R_1 ~ C ~ ln \frac{V_{cc}-V_H}{V_{cc}-V_L} = \\ R_1 ~ C ~ ln (1+R_3/R_2) $$

When \$V_{cc}\$ jumps from high to low, \$V_-\$ goes from \$V_H\$ to \$V_L\$, discharging C across \$R_1\$ and reaching low level in a time \$T_L\$ given by:

$$ V_{-}(t) ~ = ~ (0-V_H) ~ (1 ~ - ~ e^{ - t / R_1 C } ) + V_H \\ \frac{V_L}{V_H} = e^{- T_L / R_1 C} $$

thus

$$ T_L = - R_1 ~ C ~ ln \frac{V_L}{V_H} = \\ R_1 ~ C ~ ln (1+R_4/R_2) $$

note that \$T_H\$ and \$T_L\$ are controlled mainly by \$R_4\$ and \$R_3\$. Selecting appropiate values, or using a variable resistor to replace \$R_4\$ and \$R_3\$, it is possible to create a PWM (pulse wave modulator).

In an usual case \$R_2\$=\$R_3\$=\$R_4\$, the period of the wave will be:

$$ T = T_H + T_L= 2 ~ R_1 ~ C ~ ln 2 = 1.39 ~ R_1 ~ C \\ f = 0.72 / { ( R_1 ~ C ) } $$

Addendum, demonstration of exponential equations used in this answer, based on Laplace transform:

In the charging stage, \$V_o(t)=V_{cc} ~ u(t)\$:

$$ V_-(s) ~ = ~ V_o(s) ~ \frac{1/R}{1/R+Cs} ~ = ~ \frac{V_{cc}}{s(1+RCs)} \\ V_-(t) ~ = ~ (V_{cc}-V_L)~(1~ -~ e^{-t/RC})+V_L $$

In the discharging stage, \$V_o(t)=V_{cc} ~ (1-u(t))\$.