1

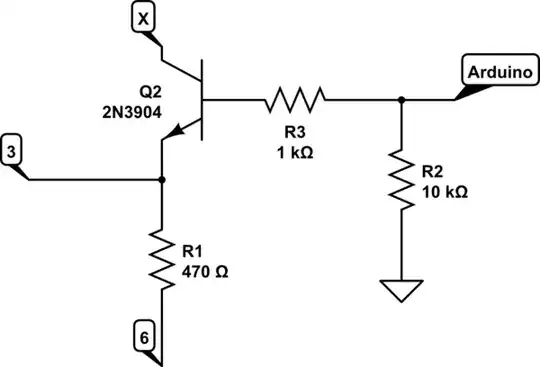
I'm having trouble with this circuit and was wondering if someone could help me. So far I know that the 20V source can be basically ignored since it is a NPN transistor here. The second circuit here is where I've gotten so far, but I'm not sure of all the values. I'm not sure what the value of the lower resistor should be. Is it still just 1k or is there something I'm missing?

enter image description here

enter image description here

Servin Vashnar
  • 137
  • 1
  • 8
  • 3
    Thevenin is for **linear circuits**, diodes and transistors are **non-linear** devices so you cannot just apply Thevenin. You could make a **small signal model** of this circuit which will be a linear representation of the circuit and then you **can** use Thevenin for that. You **cannot** ignore the 20 V because a collector current will flow and influence the behaviour. – Bimpelrekkie May 08 '17 at 20:10

2 Answers2

2

Call the emitter resistor, \$R_E\$. Just go around the loop:

$$5.6\:\textrm{V} - I_B\cdot R_B - V_{BE} - I_E\cdot R_E = 0$$

Assuming active region (reasonable here, though you should check the results when you are done to be sure about it) and knowing that \$I_E=\left(\beta+1\right)\cdot I_B\$, you can work out:

$$\begin{align*} 5.6\:\textrm{V} - I_B\cdot R_B - V_{BE} - \left(\beta+1\right)\cdot I_B\cdot R_E &= 0\\\\ 5.6\:\textrm{V} - V_{BE}&= I_B\cdot R_B - \left(\beta+1\right)\cdot I_B\cdot R_E \\\\ 5.6\:\textrm{V} - V_{BE}&= I_B\cdot\left( R_B - \left(\beta+1\right)\cdot R_E\right) \\\\ &\therefore\\\\ I_B=\frac{5.6\:\textrm{V} - V_{BE}}{ R_B - \left(\beta+1\right)\cdot R_E} \end{align*}$$

From that, you should be able to calculate anything else what you want, I think. However, it ignores the Early effect. But I don't know if you care about it, or not.

If you want, you can re-estimate \$V_{BE}\$ from the currents you work out and then work through the calculations another time to narrow it down some.

If you use \$V_{BE}\approx V_T\cdot\operatorname{ln}\left(\frac{I_C}{I_{SAT}}\right)\$, removing the \$+1\$ in the Shockley equation to simplify the result, and solve it this way:

$$\begin{align*} I_B&=\frac{5.6\:\textrm{V} - V_T\cdot\operatorname{ln}\left(\frac{\beta\cdot I_B}{I_{SAT}}\right)}{ R_B + \left(\beta+1\right)\cdot R_E}, \quad\textrm{setting: }I_T=\frac{V_T}{R_B + \left(\beta+1\right)\cdot R_E}\\\\ &\textrm{then,}\\\\ I_B&= I_T\cdot \operatorname{LambertW}\left(\frac{I_{SAT}}{\beta\cdot I_T}\cdot e^{\frac{5.6\:\textrm{V}}{V_T}}\right) \end{align*}$$

Using branch 0 of the LambertW function, I think. Then you don't have to iterate the computation. But most calculators don't include that function key.

(If you are interested in what the LambertW function is [how it is defined] and in seeing a fully worked example on how to apply it to solving problems like these, then see: Differential and Multistage Amplifiers(BJT).)

jonk
  • 77,059
  • 6
  • 73
  • 185
1

This question makes only sense if you have a linear circuit. I.e. you have to replace your non-linear diode by a linear model: this can be done if you assume that it is always forward biased and use a very simple diode model: a constant 0.6V voltage source.

Here are successive simplification steps turning your circuit into a linear circuit that consists of 2 resistors, 3 independent voltage sources and 1 dependent current source.

schematic

simulate this circuit – Schematic created using CircuitLab

Now just find its Thevenin equivalent (e.g. by applying two different test voltages and determining the current).

Curd
  • 16,043
  • 34
  • 43