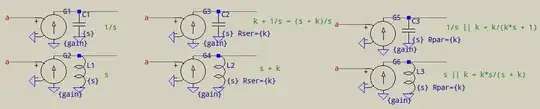2

Is there a way to take a sub circuit definition (.subckt) and have SPICE (or in my case LTSpice) take the Transfer Function for it. Then have SPICE refer to this Transfer Function whenever a component with this .subckt definition is inserted in any schematic, the transfer function is used.

As far as I know, a .subckt can only be defined as a netlist, not a Transfer Function.

The real issue is that I'm having some trouble getting my circuits converging fast enough (simulation can take tens of minutes to finish). It's probably because I'm starting to use more and more constant current sources.

Any tips?

Dehbop
  • 279
  • 7
  • 19
  • 1
    I hope you are aware that your suggestion makes only sense if the subcircuit you want to define by its transfer function is a LTI system (at least a linear system). If this is the case, however, I doubt that it takes long for SPICE to converge... In other words: if it takes long for SPICE to converge I doubt that it is because of a subcircuit than can be described by a transfer function. Probably it's because of a (highly non-linear) part you cannot replace by a transfer function. – Curd Aug 01 '17 at 14:01

1 Answers1

2

That's a good step using current sources over voltage ones. You can use transfer functions under the form of Laplace expressions, looking like this:

Laplace=(s + 1)/(s^2 + 2);

This, as seen, would be entered as the value of a G source, for example. LTspice will know to transform s into the complex exponential. It can also work in a behavioural source.

BUT while the Laplace expressions will work flawlessly in frequency domain, they can result in garbage in time domain, something mentioned in the manual.

This is why, unless you're dealing with exotic transfer functions having sqrt(s), or similar, non-multiple of s, it's better to derive your transfer functions using the basic RLC elements. For example:

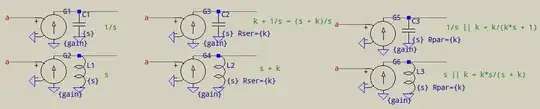
basic building blocks

These can be combined into full-sized transfer function expressions, but they should be proper transfer functions; for improper ones, you'll have to juggle with the basic building blocks above, somehow. For stability issues, it's also a good idea to split the longer expressions into 2nd order ones. Here is an example:

2nd order block

You could also use S-param files, but, IIRC, they're based on Laplace. These are just examples on how to do it and, remember, it's just to avoid the awful performance in time domain of Laplace expressions. Ultimately, the choice is in your hands.

The generic transfer function for the 2nd order block is this:

$$H(s)=\frac{a_{2}s^2+a_{1}s+a_0}{s^2+b_{1}s+b_0}$$

where \$a_n\$ and \$b_n\$ are the ones in the image, while \$s\$ is expressed as \$\frac{1}{2\pi f}\$ (since, as seen in the 1st image, G+C means \$1/s\$).

As a reminder, the transfer function should be proper: the order of the numerator is less than or equal to the denominator's.

a concerned citizen
  • 21,167
  • 1
  • 20
  • 40