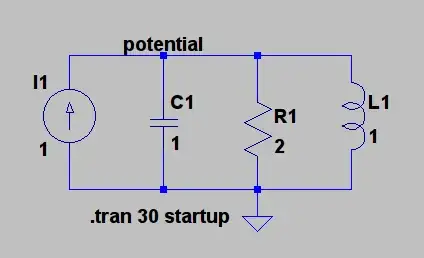
I need to find the current going through the inductor \$(I_l)\$ for \$t>0\$ using Laplace circuit analysis, to then find \$(I_l)\$ in the time domaine.
simulate this circuit – Schematic created using CircuitLab
I came up with the following way of finding \$(I_l)\$ using current divider.
\begin{align} I_L (s) &= \frac{Z_{total}}{Z_L} \cdot I_{total}(s)\\[0.7em] &= \frac{Z_C + Z_R + Z_L}{Z_L}\cdot I_{total}(s) \\[0.7em] &= \frac{s^2 + 2s + 1}{s^3} \end{align}
and then to find \$ I_L(t) \$ I would do
\begin{align} I_L (t) &= \mathcal{L}^{-1}\{I_L(s)\} \\[0.7em] &= \mathcal{L}^{-1}\left\{ \frac{s^2 + 2s + 1}{s^3} \right\}\\[0.7em] &= \frac{t^2}{2} + 2t + 1 \end{align}
Could someone please tell me if I did it the right way ?