BJT Amplifier with Emitter Bypass Capacitor Design

Question

I am trying to design a BJT amplifier. The circuit is shown below with its parameters.

• beta=180
• RL=20kΩ
• VA=0 (early effect can be ignored)
• VCC=15V

There are three constraints listed below:

1. Swing voltage of Vout must be between 22V and 24V (peak to peak)
2. Voltage gain must be equal to 20.
3. Power dissipation by resistors must be under 0.2 Watt

As you may understand this is a project and I do not expect the whole solution. But useful hints or calculation steps would be so useful. I want to learn,

• Which part of this circuit should I design first?
• How do I adjust peak to peak voltage?
• How do I approach power dissipation considerings?

Answer 1

First, start by drawing the schematic in a form that makes the circuit easier to see and easier to talk about:

Note that the resistors are just numbered. None of this silly Re1, Re2, etc. Since the output load impedance is known, it's also shown explicitly. So are the power supply voltages, and there aren't vague down arrows leaving you guessing where things are connected. Also note the junction dots. That's how it's done. Don't be sloppy.

Now some assumptions that weren't stated in the problem: No frequency response requirements were given, so that gives us no guidance what the value of the capacitors should be relative to the resistors. I'll assume this is meant to be a linear amplifier to the extent reasonably possible, and that the frequency response is meant to be flat over whatever the desired passband is.

I will therefore assume that all three caps will be so large that their impedance will be negligible compared the resistors around them at the lowest frequency of interest. From this it follows that the caps can be considered shorts to the signal, but opens to DC. That simplifies things a bit.

Now that we have a proper problem statement, here is how I would proceed:

1. Start with R3 being small compared to the load impedance. 1/10 of the load impedance is a good start. I wouldn't worry about the maximum current or resistor dissipation at this point. Start with R3 and keep working backwards until all resistors are picked, then see where you're at and adjust accordingly.

   So in this step, we pick 2 kΩ for R3.

2. Satisfy the gain constraint. I'll assume the voltage gain is specified, not the power gain or something else. Generally, unqualified "gain" of a amplifier means the voltage gain.

   Note that the voltage gain is mostly the impedance connected to the collector divided by the impedance connected to the emitter. The same current (to within 1 part in 180) flows thru the emitter load as the collector load. The voltage across each of these impedances is therefore proportional to those impedances.

   Note that the impedances above are those to the signal, which is not necessarily the same as the DC bias currents. Remember that for the signal, all caps are shorts.

   Hopefully from that you can see that the impedance on the collector is R3//R6, and on the emitter R4. You now solve for R4.

3. Solve for R5 by using the maximum output swing constraint.

   The highest the output can go is when Q1 acts like a open switch from C to E. The output voltage then is just from the voltage divider formed by R3 and R6. Find that.

   Since we want this amp to be reasonably linear, let's keep a minimum of 1 V across Q1 C to E. This is a judgement call, but I think a reasonable one.

   The maximum output swing is supposed to be 22 to 24 V. Let's aim for the middle of that, so 23 V. You already know the maximum with Q1 completely off. The minimum is therefore 23 V less. The emitter of Q1 is then 1 V less than that.

   From these voltages, you can compute the collector current, which is also the emitter current (again, to within 1 part in 180, good enough). Now you can compute the voltage across R4, which tells you the voltage at the bottom end of R4. That's the voltage across R5, which we consider fixed due to C3.

   Now you know the current thru R5 and the voltage across it, so you can compute its value.

4. Find R2 and R1 to set the DC bias point.

   Since now we're considering the steady state DC operating point, all capacitors are open for purposes of analysis. This means the the collector load is R3, and the emitter load R4+R5.

   Ideally, the amp can swing symmetrically above and below the bias point. Therefore, place the collector voltage at the midpoint of what you computed before. That tells you the collector current, which is the emitter current, which times R4+R5 yields the emitter voltage. Figure the base voltage is 700 mV above that. That's because B-E looks like a diode to the circuit, and that's about the voltage a silicon diode develops.

   You know the emitter current, so the base current is 1/180 of that.

   You know the voltage to hold the base at and how much current that takes, but you still have one degree of freedom left. That can be expressed as the impedance the base is being driven with. High impedance is good for a amplifier, but no restriction was specified in this case. The lower you make the R2,R1 output impedance, the better the bias point will be held across part variations and temperature.

   Since your instructor failed to specify a input impedance, you could make it low to make things easier on yourself. You could make it 100 Ω and argue the design meets all the specs. You'd be right, but still wrong in the end. Engineering is about solving problems, not showing that it was someone else's fault the problem didn't get solved when you were aware of the issue all along. Waving a bunch of calculations in the customer's face won't change the fact that the amplifier doesn't do what it needs to do.

   Part of your job is to fill in requirements the customer doesn't know to specify. In the real world you'd go back to the customer and understand how this amplifier will be used and what minimum input impedance it must have. You could go back to the professor and ask, or make it as high as reasonable and then explicitly state the input impedance. I'll go with the latter here.

   I'd want the R2,R1 output impedance to be no more than 1/10 of the impedance it is driving. The impedance looking into the base is the emitter load times beta+1, or 181. Note that the +1 is silly since real transistors vary much more than that from part to part. However, you have to use something to reflect the emitter load to the base, and 181 is the best value you have.

   So, the impedance looking into the base is 181(R4 + R5), for the purpose of the DC biasing network. You know that the base voltage will be near the middle of the voltage range. I'd arbitrarily pick R1 to be the nearest standard value to 181(R4 + R5). It should be obvious from inspection that the base voltage will be well towards the low end of the voltage range. That means R1 will be significantly less than R2, so the R1//R2 impedance is dominated by R1.

   Now you have R1, and the voltage across it, which means you know the current thru it. We previously found the current into the base. You know the voltage across R2, and the current thru it is the current thru R1 plus the base current, so you can compute R2.

5. Power dissipation check. This is more tricky than it may seem, and is rather clever of your professor (I'll give him the benefit of the doubt that he thought of this issue).

   The voltage across R5 is fixed, so you can compute the power outright. R2 and R1 are higher impedance, so they won't be the limiting factor. The same current flows thru R4 and R3. Since R3 is higher than R4, the only resistor you have to really watch out for is R3.

   The tricky part about R3 is that you have to consider both the DC and AC components. You know the minimum and maximum peak voltage that will be across it. It's not as simple as averaging those and calling it done.

   One way to look at the voltage on R3 is the peak-peak average with a AC component added. That AC component adds to the overall RMS voltage. You could assume the AC component is a 23 Vpp sine. However, consider what the power dissipation spec it for. It is to ensure that the resistors aren't over stressed. You really should use the worst case input that anyone could throw at this amp and make sure it won't fry itself.

   That worst case input is a square wave. You also have to assume the amp is over-driven. Stuff happens. You don't want the amp to blow up when someone cranks the input volume too high. Fortunately, this actually makes figuring the dissipation of R3 easier.

   Figure the over-driven input will cause the transistor to switch between fully off and saturated. You should also assume there is no load connected that helps dissipate power. During the Q1-off phase, R3 has no voltage across it and dissipates no power. Figure Q1 goes fully into saturation the other half the time, so has 200 mV across it. Personally, I'd not try to split hairs with the 200 mV, just call it a dead short. If you're within spec at 200 mV but not a 0 V, then you don't have enough margin for stuff to happen anyway.

   The AC assumption still holds true, so you still consider C3 to have the same fixed voltage on it as before. For the Q1-on phase, you have R3 and R4 in series connected to 30 V minus the C3 voltage. Find the dissipation of R3 with that voltage applied, than divide by two since that occurs half the time.

   If the power dissipation of R3 is too high, then make its resistance higher, go back to step 2, and derive everything else from that. You might even work backwards what the minimum R3 value can be, round up to the nearest higher standard value, and recalculate everything from that.

I didn't actually do any of these calculations, since that's your job, and I am not just going to give you the answer to a homework problem. Maybe I'll come back here in a week or so if I remember and fill in the values.

Answer 2

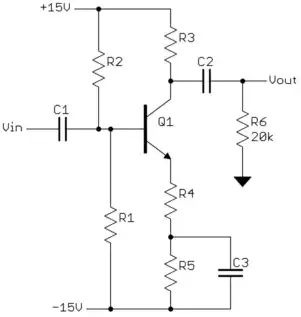
The below is an updated answer, with a complete walk-through. Others may choose to place things somewhat differently. Or may use a different order to the steps. Certainly, different biasing choices might well have been made for \$R_1\$ and \$R_2\$ as well as a different choice for \$I_{C_q}\$.

The OP should read this and then demonstrate some understanding by trying their own hand at a design using some different earlier choices than I do, below. Post that work within the question.

---

One of the first things I think about is getting the DC emitter voltage at least a volt (more is better) above the low rail. I also like to avoid letting \$\vert V_{CE} \vert \lt 2\:\textrm{V}\$ so that it stays well away from saturation. (Keeping \$\vert V_{CE} \vert \ge 4\:\textrm{V}\$ is even better, but I don't usually have that option.) Finally, I like to leave some margin against the high rail -- a volt or better.

If the peak-to-peak can be as little as \$22\:\textrm{V}\$, that leaves me plenty of room. \$24\:\textrm{V}\$ narrows that down, but it is still okay. So....

I'd like to reserve \$2\:\textrm{V}_\textrm{DC}\$ for the emitter degeneration leg, \$4\:\textrm{V}_\textrm{DC}\$ for minimum \$V_{CE}\$, and another \$1\:\textrm{V}_\textrm{DC}\$ for margin against the top rail. This leaves room for a peak-to-peak of \$23\:\textrm{V}\$. Which seems okay and gets me all the margins I might want.

Measuring relative to ground, this means:

$$\begin{align*} V_{C_q}=-15\:\textrm{V}+2\:\textrm{V}+4\:\textrm{V}+\frac{1}{2}\cdot 23\:\textrm{V}&=+2.5\:\textrm{V}\\\\ V_{E_q}= -15\:\textrm{V}+2\:\textrm{V}&=-13\:\textrm{V}\\\\ V_{B_q}= V_{E_q}+750\:\textrm{mV} &= -12.25\:\textrm{V} \end{align*}$$

---

The following was just added:

Roughly speaking, the voltage across the load is \$\frac{23\:\textrm{V}_\textrm{pp}}{2\sqrt{2}}\approx 8.1\:\textrm{V}_\textrm{RMS}\$. So the current will be about \$\frac{8.1\:\textrm{V}_\textrm{RMS}}{20\:\textrm{k}\Omega}\approx 400\:\mu\textrm{A}_\textrm{RMS}\$. I'd like the average collector current about \$20\times\$ that figure, so without considering the resistor dissipation I'd select:

$$I_{C_q}=8\:\textrm{mA}$$

This means:

$$R_C= \frac{V_{CC}-V_{C_q}}{I_{C_q}}=\frac{+15\:\textrm{V}-\left(+2.5\:\textrm{V}\right)}{8\:\textrm{mA}}\approx 1.5\:\textrm{k}\Omega$$

I don't know the input impedance and cannot therefore figure out the loss due to input loading (have to assume a very low impedance driver), but I know now that the load itself will mean I get \$\frac{20\:\textrm{k}\Omega}{20\:\textrm{k}\Omega+1.5\:\textrm{k}\Omega}\approx 93\%\$ across the load. I need to plan on a gain, then, of \$\frac{20}{.93}\ge 21.5\$ in order to achieve the specified final gain. I'll round that up to 22.

Before computing \$R_{E_1}\$, one more note. \$r_e=\frac{k T}{q I_C}=3.25\:\Omega\$. This means:

$$R_{E_1}=\frac{1.5\:\textrm{k}\Omega}{22}-r_e\approx 65\:\Omega$$

We'll round that down to a standard value of \$62\:\Omega\$ and realize that the gain may be slightly more than expected.

Normally, at this point, one might imagine it is convenient to work out the value of \$R_{E_2}\$. However, it's now actually time to work out the biasing pair, first. This is partly because one wants to use standard value resistors and the biasing point will be different than what I mentioned above for \$V_{B_q}\$.

So at this point I probably want the biasing pair to be "stiff" relative to \$I_B\$. Given \$\beta=180\$, \$I_{B_q}=\frac{I_{C_q}}{\beta}\approx 45\:\mu\textrm{A}\$. "Stiff" would be at least ten times that. But let's use something around \$I_{bias}=500-600\:\mu\textrm{A}\$ for the biasing pair and see where that goes. Shooting for a standard value:

$$\begin{align*} R_1=\frac{V_{B_q}-V_{EE}}{550\:\mu\textrm{A}}&\approx 4.7\:\textrm{k}\Omega\\\\ R_2=\frac{V_{CC}-V_{B_q}}{600\:\mu\textrm{A}}&\approx 47\:\textrm{k}\Omega \end{align*}$$

\$R_1\$ and \$R_2\$ can be combined into \$R_{TH}=R_1\vert\vert R_2\approx 4273\:\Omega\$. Then also, \$V_{TH}=-12.27\:\textrm{V}\$. From this, it follows that:

$$I_{B_q}=\frac{V_{TH}-V_{BE}-V_{EE}}{R_{TH}-\left(\beta+1\right)\cdot \left(R_{E_1}+R_{E_2}\right)}$$

But we already know \$I_{B_q}\$, so we can solve the above for:

$$R_{E_2}=\frac{1}{\beta+1}\cdot\left(\frac{V_{TH}-V_{BE}-V_{EE}}{I_{B_q}}-R_{TH}\right)-R_{E_1}\approx 157 \:\Omega$$

Round that to down \$150\:\Omega\$.

The final circuit is:

^{simulate this circuit – Schematic created using CircuitLab}

If you now use the standard resistor values shown in the schematic, plugging them back in to the above equation to find \$I_{B_q}\$, you will find that you get the value of \$I_{B_q}\approx 46\:\mu\textrm{A}\$. Very close to where we wanted it to be.

The maximum power consumption in any resistor will be in \$R_C\$. In this case, \$I_{RC_\textrm{rms}}=\sqrt{8\:\textrm{mA}^2+\frac{8.1\:\textrm{V}_\textrm{RMS}}{R_C}^2}\approx 9.7\:\textrm{mA}_\textrm{ RMS}\$. From this, I'd estimate about \$150\:\textrm{mW}\$ dissipation, in round number, for \$R_C\$. This is within the requirements.

---

The above design is arranged so that variations in the saturation current, \$I_S\$, or \$V_{BE}\$ shouldn't result in bad behavior. There's a lot of room reserved for \$V_{CE}\$ (which helps pick up for such variations.)

---

I'm just a hobbyist. So I'd also be interested to see other approaches being shown and/or criticisms of the above approach to the given topology, as well.

Answer 3

My Design Criteria:

• Rc <= RL (20k)
• Rc/Re1=20

• VRe2 drop < 4V to get 24V wing from 30V allowing 2V for Vce(min)

• Ic with Rc must achieve Vdrop ~V+ -1V for max symmetry with Vcemin=2V

• R1,R2 defines Vb which defines Ie with Re1+Re2 to achieve Vc (dc)

• so everything is derived from the load RL and Rc
• with caviets for Pd max on all R's