Finding Transfer Function, Poles, Zeros of an RC Circuit

Question

I'm trying to brush up on some electronics theory and am working through this PDF.

At the bottom of page F-6 there is a problem, F.1, that I am currently trying to solve. The circuit is as follows:

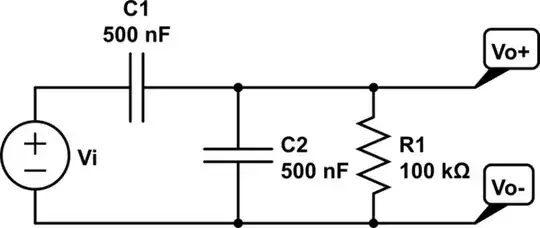
^{simulate this circuit – Schematic created using CircuitLab}

In order to find the transfer function, $$T(s) = \frac{Vo(s)}{Vi(s)}$$

I first obtained the following equivalent circuit:

^{simulate this circuit}

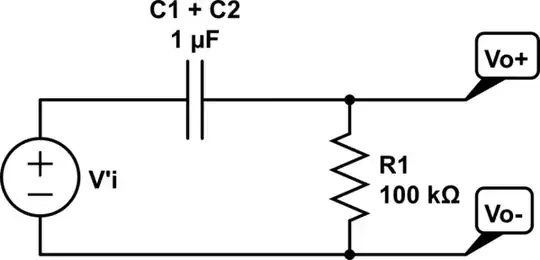
where $$V'i = \frac{Vi*C1}{C1+C2}$$

From this I get the transfer function using the Laplace transform: $$T(s) = \frac{s}{s + \frac{1}{R(C1 + C2)}}$$

At this point I'm not entirely sure if I have done everything correctly so I would like some verification. If this is not correct then please let me know so that I can edit the question showing my math. This should help us narrow down to where the mistake is. I just don't want to post all of the math unless I absolutely need to.

The second part of the question asks if this is a single time constant circuit, which I expect it is because the circuit can be reduced to a single capacitor and a single resistor. The type would be high-pass.

The third part of the question says that for the element values shown, find the poles and zeros. It is clear from the transfer function that there is a zero at s = 0 rad/sec and a pole at $$\frac{1}{R(C1+C2)} = \frac{1}{100k*2*(0.5*10^{-6})} = 10$$ rad/sec.

Are these answers all correct, and are they complete? Have I missed something? I have not done this for some time so I am in dire need of a refresher course.

EDIT:

The last part of the problem asks to sketch the magnitude and phase response Bode plots. I am having some trouble with this part. I have the following for the magnitude:

where plot A is the final gain. Did I do this part correctly? As for the phase, I'm not even sure where to begin. I have that $$Φ = -tan^{-1}(\frac{w}{10})$$ and I believe that the s = 0 term starts us off at +90°, so that would give us a straight line on the plot of degrees vs. rad/sec. I don't know where to go from there. Some assistance on this part would be appreciated. What is the next step (to plot the phase of the pole)? I know the phase would drop but where the drop begins/ends I do not know.

I am happy to provide further clarification wherever necessary.

Answer 1

Using impedances (forgive the lack of standard forms along the way) and going long-hand from scratch, I get:

$$\begin{align*} \frac{V_O}{V_I}&= \frac{R\:\vert\vert\: C_2}{C_1+R\:\vert\vert\: C_2}\\\\ &=\frac{\frac{R}{1+s R C_2}}{\frac{1}{s C_1}+\frac{R}{1+s R C_2}}\\\\&=\frac{\frac{R}{1+s R C_2}}{\frac{1+s R C_2}{s C_1 \left(1+s R C_2\right)}+\frac{s R C_1}{s C_1 \left(1+s R C_2\right)}}\\\\ &=\frac{\frac{R}{1+s R C_2}}{\frac{1+s R\cdot\left(C_1+C_2\right)}{s C_1 \left(1+s R C_2\right)}}=\frac{R}{1+s R C_2}\cdot\frac{s C_1 \left(1+s R C_2\right)}{1+s R\cdot\left(C_1+C_2\right)}\\\\&=\frac{s R C_1}{1+s R\cdot\left(C_1+C_2\right)}=\frac{\frac{s C_1}{C_1+C_2}}{s+\frac{1}{R\cdot\left(C_1+C_2\right)}}\\\\&=\left[\frac{s}{s+\frac{1}{R\cdot\left(C_1+C_2\right)}}\right]\cdot\left[\frac{C_1}{C_1+C_2}\right] \end{align*}$$

So I guess I agree with your results (in the first part.)

Answer 2

A contribution: Regarding to the math, I believe the easiest way to get the transfer function \$V_o(s)/V_i(s)\$ is to apply the KCL to the top node:

Answer 3

You pole and zero are correct, but the transfer function should be T(s) = sRC/(s2RC+1). Rearranged, your transfer function would be T(s) = s2RC/(s2RC +1). You didn't show all your steps, so I can't see where you went wrong.