This answer ----- The amplitude of the phase noise (in µs) is simply the noise voltage divided by the slope ----- is from Dave Tweed.
Or
$$TimeJitter = Vnoise / SlewRate$$
is the form I've used for over 2 decades.
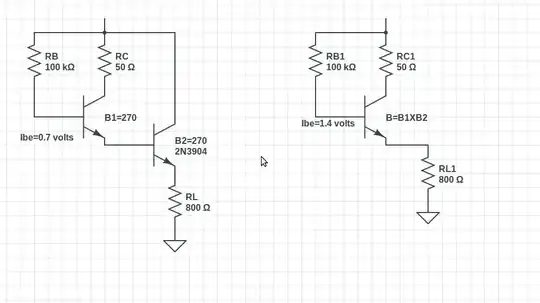
I worked at a walkie-talkie company, who had converted from tiny 50_ohm RF modules to integrated circuits. Much less power demand, much longer battery life. But the close-in phase noise preventing shipping the product, because the transmitter would de-sensitize any nearby receiver; they needed a phasenoise level of -150dbc/rtHz and had no idea how to fix their problem. Line DOWN. No shipping. Using the above formula, and making assumptions about their frequency synthesizer's prescaler and the rbb' of the prescaler bipolar current-steering devices, we predicted the total Rnoise of the prescaler had to be less than 6,000 ohms. We were selectively burning power, only where the math/physics predicts power must be burned.
In ONNN Semi PECL, using Bandwidth of 10GegaHertz and Rnoise of 60 Ohm (1nV/rtHz), with Slewrate of 0.8v/40picoseconds, the TimeJitter is
Vnoise = 1nV * sqrt(10^10) = 1nV * 10^5 = 100 microVolts RMS.
SlewRate is 20 volts/nanosecond.
The TimeJitter is 100uV RMS / (20v/nS) = 5 * 10^-6 * 10^-9 = 5 * 10^-15 seconds RMS.
What is the spectral density of the jitter? We simply scale down by the sqrt(BW) which is 10^5, yielding 5 * 10^-20 seconds/rtHz.
For your question: 1MHz, 1voltPeak, 20dB SNR and Tj = Vnoise/SR, we have
Vnoise = 1V/10 = 0.1vRMS (ignoring any sin-peak-rms ratios)
SlewRate = 6.3 Million volts/second, therefor
TimeJitter = 0.1v/6.3Mega v/Sec = 0.1 * 0.16e-6 = 0.016e-6 = 16 nanoSeconds RMS.
EDIT/ENHANCE: converting a sin into a squarewave. One of the most risky of these is converting a CrystalOscillator sin into a rail-rail squarewave. Any casualness, or unawareness of the hidden trash generators, results in the typical jittery microcontroller clock. Unless the entire signal chain, from XTAL interface thru amplifiers and squarers and clock-distribution are provided private power rails, you end up with apparently random clock-timing upsets but not random at all, instead dependent on VDD collapses triggered by program-related energy demands. All of the circuits that touch, or bias any circuit that touches, the clock edge, should be analyzed using
$$Tjitter = Vnoise/SlewRate$$
The ESD structures are a problem. Why allow 3pF capacitors (the ESD diodes) to couple MCU-program-related energy-demand events into the clean sin from the CRYSTAL? Use private VDD/GND. And design the substrate and wells for charge control. To cross from XTAL domain into MCU domain, use differential current steering with a 3rd wire to pass along the expected trip points.
How serious is this? Consider typical MCU ringing to be 0.5 voltsPP. Running that into a 3pF ESD and then into a 27pF Cpi, we get a 10:1 reduction (ignoring any inductance), or 0.05 voltPP imposed atop the 2voltPP crystal sin. At 10MHz
sin, the SlewRate --- d(1*sin(1e+7 * 2pi*t))/dt --- is 63MegaVolts / second. Our Vnoise is 0.05. The jitter right at that point in time is
Tj = Vn/SR = 0.05 volt / 63e+6 volt/sec == 0.05 / 0.063e+9 ~~ 1 nanosecond Tj.
What if you use a PLL to multiply that 10MHz up to 400MHz for MCU clock? Assume the divide-by-400 FlipFlops (8 of them) have 10Kohm Rnoise, with 50 picosecond edges over 2 volts. Assume the FFs have 1/(2*50pS) = 10GHz bandwidth.
Random noise density FF is 12nanoVolts/rtHz (4nv * sqrt(10Kohm/1Kohm)). Total integrated noise is sqrt(BW) * 12nV = sqrt(10^10Hz) * 12nV = 10^5 * 1.2e-9 == 1.2e-4 = 120 microVolts rms per FF. 8FF are sqrt(8) larger. We'll assume some gate noise, and make the factor sqrt(9): 120uV*3 == 360uVrms.
SlewRate is 25 picoseconds/volt or 40Billion Volts/second.
Tj = Vn/SR = 0.36milliVolts/40Billion volts/second = 0.36e-3/0.04e+12 = 9e-15 seconds Tj.
Seems rather clean, right? Except the FlipFlips have ZERO ability to reject VDD trash. And substrate trash is looking for a home.