If it was per unit length, I'd understand, but apparently it is a constant of the whole line.
Consider if I change the length of the transmission line, the impedance of the whole thing should increase since more power is dissipated, but the characteristic impedance doesn't change. So, what exactly is the characteristic impedance?
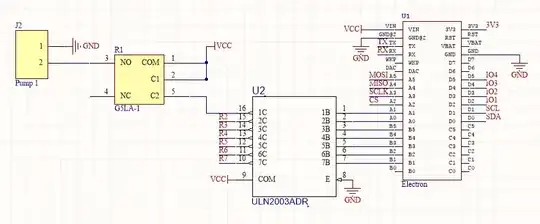
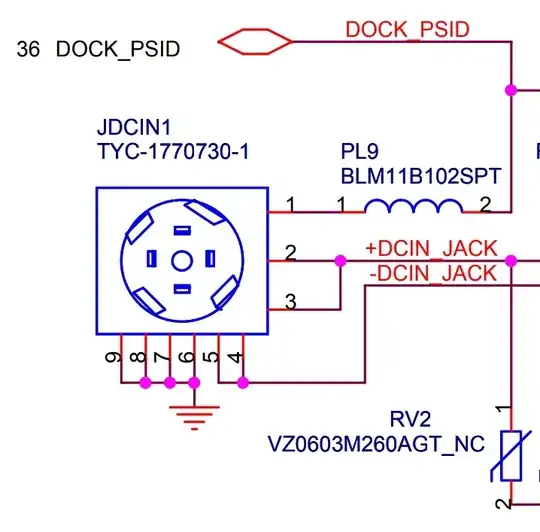
At a risk of collecting few negative points, I will try to answer this question as follows:
The "characteristic impedance" has no direct physical meaning. It is just a constant in amplitude coefficients in the solution to the "Telegrapher's Equation", which describes propagation of a sinusoidal electromagnetic wave(s) along a special geometry of uniform conductors called "transmission line". The equation is a derivative from more general Maxwell Equations.
The actual amplitudes of propagating EM waves are determined by "boundary conditions" to the line, by impedance of driver, and impedance of receiver (terminations).
Formally, the ratio of V(t)/I(t) defines the “characteristic impedance” of an ideal (lossless) transmission line, which appears to be a real (non-imaginary) number, just like an ordinary passive resistor. One might think that this resistor must dissipate Joule heat.
In other words, Z=V(t)/I(t); I(t) = V(t)/Z; P = V*I = (V^2)/Z. V is a real function of t, Z is real, so P must be non-zero, and must dissipate into heat. But in this case the wave should quickly disappear. However, it is known that the ideal transmission line doesn’t dissipate anything, and waves can propagate forever to infinity. Therefore, we have an obvious paradox: we have seemingly a real “impedance”, but it doesn’t dissipate any energy.
The resolution of this paradox is this: formally and accurately, the Joule dissipation occurs only when a current FLOWS ACROSS A RESISTOR. The trick is that in the case of transmission line no current is flowing across the “characteristic impedance”. If one to examine the excellent animation in the referenced Wikipedia page, one can see that the current oscillates ALONG the conductors of transmission line, not across the empty space between conductors. The actual impedance across the conductor gap is infinitely large, and no dissipation occurs. The electrons are moving back and forth along the wires that are assumed to be perfect conductors, so no energy is dissipated there as well.
In different words, formally one can take any V(t) from a circuit, and divide it by I(t) from any node. The result will be a number in units of resistance, but it may mean nothing. In case of “characteristic impedance” the V/I ratio is just that, a characteristic of transmission line geometry/permeability, and does not represent the current across the transmission line.
The characteristic impedance however can serve an important mission: if the termination is purely active (real restive) and equal to the characteristic impedance, the resulting wave solution does not have the reflected wave, which is very useful in design of high-speed electronics (and in power lines as well).
You seem to confuse two concepts:
Attenuation is the amount of something (in this case electrical energy) that is absorbed by a medium. Attenuation is linear with the distance.
Reflection is something (in this case again electrical energy) that is emitted by the source, but not absorbed (accepted, trasmitted, ...) by the medium. Instead it is reflected back.
Reflection is caused by a mismatch between the source (driver) impedance and the destination(medium) impedance. When both are the same no reflection occurs, and all energy is 'acceppted' by the medium.
The characteristic impedance is the impedance of an infinitely long transmission line. When you drive such a transmission line, you likely want to match the impedance of your driver to taht of the transmission line, to avoid reflection (which is, at best, a waste of energy).
In practice, a transmission line doesn't need to be infinitely long to have almost the same characteristic impedance of an infinitely long one, a few wavelengths is often sufficient. Henec it is a very usefull characteristic to know.
The characteristic impedance is defined for every point on the line. In a good line, it's constant along the entire length, and much effort is spent by connector manufacturers to maintain the impedance constant even through the connector. In a bad line, it varies from point to point, and can become very different at connectors.
As a wave propagates along a transmission line, it consists of a voltage wave, which is the voltage of one conductor with respect to the other, and a current wave, which is the out-flowing current in one conductor and the return current in the other.
The characteristic impedance is the ratio of wave voltage to wave current at each point along the line.
Physically, the characteristic impedance depends on the cross-sectional geometry of the line, which controls the shunt capacitance per unit length, and the series inductance per unit length of the line. The impedance is sqrt(L/C) at any point, where L and C are the per unit length values for the capacitance and inductance.
In a coaxial cable with conductor radii R_inner and R_outer, the capacitance, inductance, and so impedance, are all proportional to the log(R_outer/R_inner).
The cross section Now we see why a line must have a constant impedance to be called good. If the impedance varies along the line, then the ratio of the volts/current of the wave must vary as it travels along the line as well. The only mechanism nature has available for doing this is to reflect some of the energy back to the source when the impedance changes, in the right phase and amplitude to make up the difference between the old and new voltage and current values.
Now we also see why terminating a line in a resistor equal in value to the line characteristic impedance is good. We know the wave coming out of a (for example) 50ohm line has that ratio between voltage and current. If fed into a 50ohm resistor, the conditions match perfectly, and all the energy in the wave is absorbed in the resistor without reflection.
If a line is terminated in an open circuit, then the current cannot flow. Nature sorts that out by reflecting an anti-phase current wave of the same amplitude, which adds up to zero current at the open circuit. Of course that current wave has a voltage wave with it, which doubles the voltage at the open circuit end as it's in phase with the incident voltage wave.
The impedance of a transmission line is the square root of the ratio between L and C. Given the line is uniform, L and C increase with line length but their ratio stays the same. That's why the impedance is constant for a uniform line of arbitrary length.
Consider if I change the length of the transmission line, the impedance of the whole thing should increase since more power is dissipated,
Power isn't really fundamentally relevant here, but let's run with it for a moment: More power is dissipated along the length of the line, and less power comes out the other end of the line. But the amount of power put into the line by the source is unchanged.
That's how you should think about the characteristic impedance: it's a property of any end of the line, which is independent of how much length of line is behind that end (or port).
That property is that the end of the line behaves the same in response to an applied voltage, as a resistor of the same value as the characteristic impedance. But that doesn't mean that the line is dissipating the power like a resistor would: it's moving it instead.
Ohms don't mean dissipation, they mean a voltage/current relationship.
An intuitive approach but nothing more!:
If you agree that the charactertic imepdance of a transmission line is defined as the ratio of the voltage wave divided by current wave at any POINT, then it is easy to see intuitively why this is constant.
When I say POINT, i an literarly refering to an infestesimally small length of the transmission line.
So as a mental picture you can imagine the transmission line made up of many fictitious resistors of value equal to the characteristic imepdance. So when you refer to the characteristic impedance you are refering to simply ONE of that fictitious resistors value. See the photo below:
Do you now see why the characteristic impedance is independant of the length of the line and independant of the POINT of measurement? (Because changing the length of the line merely changes the number of copies of the fictitious resistors but not their value and hence the characteristic impedance)
A cable (or generally transmission line) can be modelled as infinite number of LC stages. So per meter you have inductance or capacitance. But the LC itself is constant.
By the way, if you have infinite transmission line, you can measure characteristic impedance with just ohm meter. It applies certain voltage and current becomes V/Z0, but never changes, as it must charge all infinite LC and will never reach the end of the line.
What is the physical meaning of the characteristic impedance of a transmission line?
Thought experiment: -
If you took an infinite length of 50 ohm coax and applied 1 volt dc at one end, what curent flows: -
One of the answers is right and one is wrong.
When you make a radio frequency transmitter and a transmit a signal onto an antenna, does power get emitted into space by the antenna or, will that only happen when there is a receiver capable of receiving something?
Hint: free space has an impedance of 377 ohms.
So, what exactly is the characteristic impedance?
For free space it is the square root of the ratio of magnetic permability (\$\mu_0\$) to electric permittivity (\$\varepsilon_0\$) : -
This also forces the ratio of electric field and magnetic field to be 377:1 (\$120\pi\$).
For space, coax or any transmission line, the same principle is involved; henries per metre (\$\mu\$) are divided by farads per metre (\$\varepsilon\$) and square rooted.
