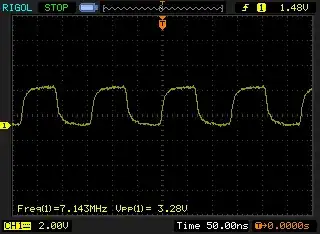
Whilst looking for a circuit to test some unidentified RF filters and coils I have lying about, I came across a FET based common drain Colpitts used in this Youtube channel hosted by RF enthusiast radiofun232 (https://www.youtube.com/watch?v=Ng49kGF3n8o).
A screenshot of the LTspice simulation is shown below. Notice the frequency. By my calculation, this oscillator should be oscillating at a frequency of about 77 kHz. Instead it oscillates at 300 kHz. If I substitute a resistor in place of \$L_2\$, it oscillates at the frequency predicted by the standard formula $$\frac{1}{2\pi\sqrt{LC_t}} \approx 77\text{ kHz}$$
I calculated the 250uH \$L_2\$ value using an online calculator and feeding in the specification given by Ko: 330 turns of "ape hair" and 6mm diameter air core.
Clearly, \$L_2\$ is affecting the frequency. I tried a number of "obvious" alterations to the standard formula, such as paralleling \$L_1\$ and \$L_2\$ - but I still didn't get 300 kHz (or near it). So, it was time to develop the transfer function including L2.
This document (Pota) provides a good analysis of the standard CC Colpitts and I used the same methodology.
The AC model I used is given above and is an alteration of the Pota model to include \$L_2\$. The KCL equation thus includes \$L_2\$ and the resulting transfer function is as follows:
and here's the full working using Maxima (the last step combines Vo with Vx/Vi to give Vo/Vi):
When I substituted \$j\omega\$ for \$s\$ and took the imaginary part to zero, I got $$\frac{1}{2\pi\sqrt{L_1C}}$$ which is clearly wrong. One thing I noticed was that the new transfer function includes an imaginary term in the numerator, that wasn't present in the original TF. I'm a little out of my depth with all this stuff and while the insights are plenty, I'm still not at a level to grasp all of this.
So, my simple questions are, where did I go wrong and how do I get the frequency I'm after?