I have searched past questions and answers on this platform but none answers this question. A prof said it is possible to sample below Nyquist rate under certain conditions. I will like to know, first, if it is possible to do this, if so, when?
-
13when you are not interest in reconstructing the waveform. – Jan 15 '17 at 13:14
-
2The answers below offer one take on your question; when I read your question, the first thought that came to mind was that your instructor was referring to sub Nyquist sampling of _sparse_ signals. There are plenty of papers on this topic; see, e.g., [Mishali, Moshe, and Yonina C. Eldar. "From theory to practice: Sub-Nyquist sampling of sparse wideband analog signals."](https://arxiv.org/pdf/0902.4291.pdf) (You might also want to consider asking a separate, more focused question on DSP.SE, if the sparse angle is what you are after.) – Mad Jack Jan 15 '17 at 21:17
-
2@JonRB, assuming you have an FM mono radio signal on a 100MHz carrier, do you really think you need to sample it at 200MHz+? – Vladimir Cravero Jan 16 '17 at 12:18
-
3Permitted by whom? I'm pretty sure I can sample at any rate of my choosing, in the privacy of my own home. – David Richerby Jan 16 '17 at 17:14
-
@VladimirCravero If you want to digitally sample a FM signal modulated on a 100MHz carrier, and reconstruct faithfully, you would need to sample it at 2GHz+. 200MHz is the minimum sampling rate you will need to guarantee that you can reconstruct a continuous sine. Realistically, if you are buying an oscilloscope for example, you will want a sampling frequency at the very least 6 to 10 times the maximum frequency you need to measure. Otherwise you lose a lot of details from the waveform! – Drunken Code Monkey Jan 16 '17 at 20:28
-
Alternatively, you could use a phase-locked loop to downconvert your signal of interest to a lower frequency, and measure that. This is what is done almost everywhere, there is very rarely any A/D conversion done at the original carrier frequency. – Drunken Code Monkey Jan 16 '17 at 20:37
-
1@DrunkenCodeMonkey No. The bandwidth of a commercial FM signal is 300kHz, so a sample rate of 600kHz would be sufficient. – user207421 Jan 16 '17 at 23:18
-
1@EJP, no, 600kHz is not sufficient right away. To be so, you need to downconvert the signal using "complex demodulation" technique first, using, say, analog 4-quadrant multiplication with a carrier frequency (aka "heterodyne"), then filter the result on both channels to 300kHz, only then the 600kHz digitizing will be sufficient. – Ale..chenski Feb 04 '17 at 00:33
9 Answers
First of all, let's get rid of the Nyquist rate misconception.
People are usually taught that the minimum sampling frequency needs to be twice the frequency of the highest frequency in the signal. This is completely false!
What is true is that if you have a "full" spectrum, and by full, I mean that it completely uses up all frequencies between the lower edge of its bandwidth and the upper edge of its bandwidth, then you need to have the sampling frequency that is at least twice the bandwidth of the signal.
So in the picture here, the sampling frequency needs to be at least 2*(Fh-Fl) in order to get the spectrum.
You also need to keep in mind that, after you do the sampling, all information about the actual frequency is lost in the sampled signal. This is where the entire story about the Nyquist frequency comes into play. If the sampling frequency is twice the highest frequency of the signal, then we can safely assume (as we're often trained to do subconsciously) that all the frequencies in the sampled signal are between zero and one half of the sampling frequency.
In reality, the spectrum of the sampled signal is periodic around Fs/2 and we can use that periodicity in order to achieve lower sampling rates.
Take a look at the following picture:
The area between the 0 and Fs/2 is the so-called first Nyquist zone. This is the area where we're doing the "traditional" sampling. Next take a look at the area between the Fs/2 and Fs. This is the second Nyquist zone. If we have any signals in this area, their spectrum will be sampled and its spectrum will be flipped, that is to say, the high and the low frequencies will be inverted. Next, we have the third Nyquist zone, between the Fs and 3Fs/2. Signals here, when sampled, will look as if they came from the first zone and their spectrum will be normal. The same goes for all the other zones, with the rule being that the spectrum of odd-numbered zones is normal and the spectrum of even-numbered zones is inverted.
Now this goes against the "traditional" rules about aliasing, since aliasing is usually taught as some evil monster coming to eat your signals away and that you have to use the low-pass anti-aliasing filters to get rid of it. In real life, this isn't how things really work. The anti-aliasing filters can't actually prevent aliasing, they just bring it down to the level where it doesn't matter any more.
What we really want to do instead is to eliminate any strong signal from Nyquist zones that are not of interest and let through the signals from the Nyquist zone that is of interest to us. If we're in the first zone, then a low-pass filter is fine, but for all the other zones, we need a band-pas filter that will allow us to get the useful signals from that zone and remove junk that we don't need that's coming from the other zones.
So let's take a look at this example:

Here we have a signal in the third Nyquist zone that is being let through by a band-pass filter. Our ADC will need to only have the sampling frequency of twice the bandwidth of the signal to reconstruct it, but we always need to keep in mind that this is actually a signal from the third zone, when we need to calculate the frequencies inside of our signal. This procedure is often called bandpass sampling or undersampling.
Now, after all this exposition, to answer your question when:
Well, let's take a look at radio, perhaps something in the microwave spectrum, maybe WiFi. A typical old-style WiFi channel might have 20 MHz of bandwidth, but the carrier frequency would be around 2.4 GHz. So, if we take our naive approach to sampling the signal directly, we'd need a 5 GHz ADC to see our signal, even though we're only interested in particular 20 MHz of spectrum. A 5 GHz analog to digital converter is something that is very complicated and expensive and it requires very complicated and expensive design too. On the other hand, a 40 MHz ADC is something that is not as "magical" as a 5 GHz ADC.
One thing that needs to be kept in mind is that, although we could in theory capture out signal with a 40 MHz ADC, we'd need very sharp anti-aliasing filters, so in practice we don't really want to run the sampling frequency too close to the bandwidth. Another thing that's also overlooked is that the circuitry of a real-life ADC behaves as a filter on its own. The filtering effects of an ADC need to be taken into account when doing band-pass sampling. Quite often, there are special ADCs with bandwidths much wider than the sampling rate that are specifically designed with band-pass sampling in mind.
Finally, there's the other side of the story as well called compressed sensing. I'm not an expert in that, and it's something that's still a bit new, but the basic idea is that if certain assumptions are fulfilled (such as that the spectrum is sparse), we can sample at frequencies even lower than twice the bandwidth of the signal.
- 23,261
- 25
- 110
- 186
-
Nice! I like the fact that you took the time to draw nice diagrams :) complements very nicely with my answer! (Yours is better, though) – Marcus Müller Jan 15 '17 at 13:40
-
By the way, I'd love to see you more often on dsp.stackexchange.com :) – Marcus Müller Jan 15 '17 at 13:57
-
@Marcus Müller I'd love to be there more often, but there's waaaay to many experts there for me to make an impact. :D Still, I'll do my best to try, especially since I'm going to be (hopefully) switching to a DSP field soon. By the way, about the diagrams... Well, there's a downside to them as well. Right now, I always have to carry a tiny notebook and a pen with me, since I've completely forgotten how to explain things without diagrams. :) – AndrejaKo Jan 15 '17 at 14:01
-
2Heh, I do scribble a lot of diagrams all day when explaining stuff to people. I really believe that the rough drawing is the primary language of the engineer :) – Marcus Müller Jan 15 '17 at 14:03
-
2
-
2in your example scenario, does a "20 MHz ADC" *sample* at 20 MHz, or sample at 40 MHz? But previously, you state that a "5 GHz ADC" is required to convert a 2.4 GHz carrier. So I'm inferring a "20 MHz ADC" means 20 Meg sample-per-second. Something's not right: fs = 2*BW. – glen_geek Jan 15 '17 at 16:42
-
1In the days before digital scopes, some companies made "sampling scopes" which would use an analog sample and hold with a short capture time, so that if one knew the input had e.g. only content between 10.02MHz and 10.03MHz, one could sample at 10.000Mhz and see a signal in the 20KHz to 30KHz range. If the sample rate was well calibrated, one could measure the frequency off the scope screen more accurately than one could measure such frequency off the screen directly. – supercat Jan 15 '17 at 17:52
-
@glen_geek You are of course 100% correct! What I had in my head at the time was the IQ sampling as mentioned in answer from Marcus Müller. I'll fix it right away. – AndrejaKo Jan 15 '17 at 18:55
-
Are you sure you meant subcutaneously and not subconsciously? I've never heard of the former used in this manner. – etarion Jan 16 '17 at 12:29
-
@etarion :D As you can see, I've been relying a bit too much on the spell-checker! – AndrejaKo Jan 16 '17 at 14:01
-
1+1; very good answer. I would only add one thing to your discussion at the end about sampling WiFi using a 40 MHz ADC. While this is possible in principle, in practice you would **not** want to try to sample a signal in the ~120th Nyquist zone. Undersampling is a common technique, but in practical systems it's typically limited to second or third Nyquist zone sampling (and maybe the fourth). As the signal increases in frequency, the deleterious effect of ADC clock jitter becomes proportionally worse. You wouldn't be able to find a 40 MSPS ADC with 2.4 GHz analog bandwidth, anyway. – Jason R Jan 16 '17 at 14:40
-
1-1: the answer is dangerously misleading. The Nyquist is not "completely false", as asserted in the beginning. The assertion that the Nuqyist sampling could be excessive is true only **if there is a prior knowledge** that the signal spectrum has certain narrow properties - limited and narrow bandwidth. Then you can do undersmapling, or random sampling, and be fine. Even if the answer has certain "if"s, this upfront general assertion about "misconception" is very damaging when coming from an engineer or scientist, and is frequently brutally misused in some shoddy sciences as climatology. – Ale..chenski Feb 03 '17 at 20:54
-
@Ali Chen Well my opinion is that sampling a signal is only possible if there is actual prior knowledge about the expected signal bandwidth. If there's none, then there's no point in doing sampling, because sampling frequency would need to be determined, and that's not very simple to do without bandwidth assumptions. – AndrejaKo Feb 03 '17 at 21:04
-
@Andrej, No, there is a standard scientific approach without prior assumptions. If dealing with uncharacterized object, people apply fast sampling first, to determine its properties, even in a crude form. Then reduce the sampling rate if deemed appropriate. Your answer is formally correct (considering all "ifs" in your text), but the upfront accent/emphasis is wrong. – Ale..chenski Feb 03 '17 at 21:21
-
@Ali Che Well, I disagree. When I talk to a neurologist about sampling rates, he'll tell me that 5 kHz is a needlessly high sampling rate. On the other hand, I'm pretty sure that an audio engineer would consider it quite non-standard and too low to be of any use, while an RF engineer might thing I actually meant 5 MHz and made a typo. In fact, in some fields, there was even a long debate about actual bandwidth of certain signals (again neurology comes to mind). This is especially the case when you have a narrow bandwidth signal of interest within wide bandwidth signal of no interest. – AndrejaKo Feb 03 '17 at 22:07
-
@Andrej, yep, this is exactly what I mean - neurologists, cardiologists, climatologists - all, being at the bottom of comprehension of mathematics, are being misled by statements like yours, that rigorous means of exact science are not applicable to their "special" fields. Woo-doo pseudoscience. The Alpha /Beta /whatever "rythms" are perfect examples of this baloney. The statement "narrow bandwidth of signal of interest within broad spectrum of signal of no interest" is a perfect example of nonsense, since this "conditional sampling" is totally subjective leading to preconceived conclusions. – Ale..chenski Feb 03 '17 at 22:36
So, many people, including professors, are confused about what Nyquist rate is:
Nyquist rate is the sample rate that you need to have to sample a signal to avoid damaging it by aliasing
What that means is that for real-valued signals and real-valued sampling, the sampling rate must be more than two times the bandwidth of the analog signal.
That means that with a 6 kHz sampling rate, you can get a 100% representation of any 3 kHz-wide band.
It does not mean that the sampling rate needs to be twice the highest frequency in the signal. If your 3 kHz, for example, are the band between 9 kHz and 12 kHz, you do not have to sample at 2·12 kHz = 24 kHz; 6 kHz is totally enough to unambigously represent the signal digitally. You would still need to know that your 3 kHz were centered around 10.5 kHz, if you wanted to later relate it to other signals, but usually, that doesn't matter.
We call this technique undersampling, and it works beautifully, and is a 100% standard technique with many technical applications. All you need to be sure is that everything your ADC (analog-to-digital converter) sees is bandlimited to half its sampling rate – that means, in the aforementioned example, that you must be sure that there's no signal below 9 kHz and no signal above 12 kHz.
advanced comments
complex baseband
Notice that this is true for real-valued sampling only. If you used things like IQ demodulators (also known as direct conversion mixers, quadrature demodulators) to give you complex, equivalent baseband, you get two streams of synchronous samples. In that case, the factor of 2 falls away. This is a very important aspect for software defined radio.
polyphase structures
If you're in the later parts of a DSP course, your professor might have hinted at the fact that you can implement things like rational resamplers, where you'd normally have to upsample by a factor of M, then filter to erase all images (filter runs at input rate · M) , then filter to avoid all aliases (filter runs at input rate · M) before downsampling by N, with a single filter that effectively runs at 1/N of the input rate – which is actually sub-Nyquist sampling. But that would basically be one of the highlights of a polyphase/multirate systems lecture, and I doubt he'd put that out there in a beginner's course – it's just too confusing.
- 88,280
- 5
- 131
- 237
Never. But you need to make sure you understand exactly what the "Nyquist rate" actually is.
Nyquist stated that you you can reconstruct the signal as long it is sampled at a rate that is more than twice the bandwidth of the signal. That bandwidth may or may not start at DC, but many sources on this topic assume that it always does, and that the highest frequency component of the signal determines the Nyquist rate.
For example, if you have an AM broadcast signal at 1 MHz that is bandlimited to ±10 kHz, the Nyquist rate for it is 2 × 20 kHz = 40 kHz, not 2 × 1.01 MHz = 2.02 MHz.
- 168,369
- 17
- 228
- 393
-
@user287001: That's true only if you assume that the sidebands are identical (pure AM). With the various AM stereo systems and/or hybrid analog/digital signals ([IBOC](https://en.m.wikipedia.org/wiki/In-band_on-channel#AM_methods)), etc., that is not a valid assumption. And no, the carrier adds no information, so I don't know why you think that "including it" suddenly increases the bandwidth so dramatically. – Dave Tweed Jan 17 '17 at 12:56
-
BTW samples at Fs > 2,02 MHz saves the fact that the signal was around 1 MHz - only needs to know additionally that no aliasing occurs.. – Jan 17 '17 at 13:51
-
+1 for "never". However, the contradiction (massive confusion) is that the Nyquist sampling does evaluate (estimate) the signal straight from DC up to f/2. **From DC**. Therefore if the signal doesn't start at DC, it can be downconverted, and only then the sampling rate can be reduced. So the answer is still "Never". – Ale..chenski Feb 04 '17 at 00:47
A prof said it is possible to sample below Nyquist rate under certain conditions.
If all you are interested in is calculating the RMS value of a waveform then you can sample below nyquist: -
The blue waveform is also a sinewave having the same RMS value as the original. What you should avoid is this: -
Exactly two sampes are taken every cycle and it's impossible to know if the aliased signal was in fact the red waveform or the green waveform.
-
That's right - you're sub-nyquist sampling the waveform, but you're super-nyquist sampling the RMS, if you want so. Anyways, you've found an application where aliasing (most of the time) doesn't hurt. But what if \$f_\text{sample}\equiv f_\text{signal}\$? – Marcus Müller Jan 15 '17 at 16:48
-
-
Wouldn't your RMS value than just happen to depend on the phase at which your sampling occurs? i.e. if you have bad luck, you might end up "looking" at zero crossings or peaks only. – Marcus Müller Jan 15 '17 at 17:29
-
1@MarcusMüller: More to the point, the portion of a signal at some given frequency will be indistinguishable from that of any other frequency which is shifted up or down by an integer multiple of the sample rate. If one is sampling at 100Hz, a 60Hz signal will appear like a 40Hz signal. If a 40hz signal would be okay, great. But a signal at 99, 101, 199, 201, etc. Hz would appear as a 1Hz signal, and a signal at 99.99Hz would appear as a 0.01Hz signal. – supercat Jan 15 '17 at 17:48
-
Sampling and base frequency have to be different and not at an integer division. I'm not saying it is necessarily straightforward or even desirable, I'm just pointing out it is possible. The second picture in my answer alludes to the potential drawback. – Andy aka Jan 15 '17 at 18:07
-
@Andyaka: Problems can occur near odd sub-multiples of the sampling rate, which I should have mentioned (I really botched my example), but the point I was trying to make is that if one is sampling at e.g. 1000Hz in the hopes of capturing the RMS amplitude of a signal that happens to be 950Hz, one must be able to capture the RMS aplitude of a 50Hz signal because that's what one will see. – supercat Jan 15 '17 at 20:15
-
-
@Andyaka: If the RMS averaging logic would report a 50Hz signal as a steady RMS level, aliasing will not pose a problem. If a 50Hz signal would be reported as a signal whose RMS level increases and decreases at a rate of 100Hz, however, then a steady 950Hz signal would be reported likewise. – supercat Jan 15 '17 at 20:18
The nyquist criterion tells you how often you need to sample in order to reconstruct a signal that is band limited. However, no physical signals are band limited, this is just an idealization. Other schemes will work for sampling other idealized signals. By giving you a-priori information about a signal, ( that it is band limited), Nyquist tells you how to reconstruct the entire signal from a few samples. If I give you different a-priori information, you can do better than nyquist. Here is an example: my idealized signals are piece wise linear. One only needs to sample these signals at their inflection points: many fewer samples than one neeeds for band limited signals. To reconstruct the whole signal, draw straight lines between the sample points. You can call this the "Linequist" criterion.:)
- 21
- 1
A periodic signal can be sampled by using sub-Nyquist sampling rate. This is well exploited in oscilloscopes. There one sample is saved for each signal repetition, but at a different position of the period. Need 512 samples? then 512 full perions of the signal is needed.
The accuracy:
Its easy to see that a stationary sinewave can be captured this way. But those 512 samples must cover the signal. That's true if 256th and upper harmonics can be considered as zeros.
This is sometimes intentionally done, eg in a sampling oscilloscope (not the same as a DSO, though some DSOs also are sampling - but a sampling oscilloscope can be an entirely analog device and they have been built since the 1950s), to deal with periodic signals that are too high in frequency to be economic to amplify or otherwise treat with linear circuitry - not many oscilloscope CRTs exist(ed) that can deal with a 1GHz signal raw (some do exist!), however 1GHz was easy to deal with by undersampling even with 1960s technology. In the end, the whole system behaves similar (not identical) to a heterodyning receiver. While there is no continous wave high frequency LO, there is still a very high frequency component hidden (and used) in the sampling clock used: It needs to be an extremely fast risetime pulse and/or whatever is used as a sampling gate needs to react to it in a fast, abrupt manner.
Obviously, a non-periodic signal cannot be examined that way, and a signal with added much lower frequency components can be thoroughly misrepresented and/or misinterpreted.
- 3,085
- 9
- 13
I think that what [rackandboneman] said is consistent with the professor's intention. The 'certain condition' would be that the original signal should be periodic.
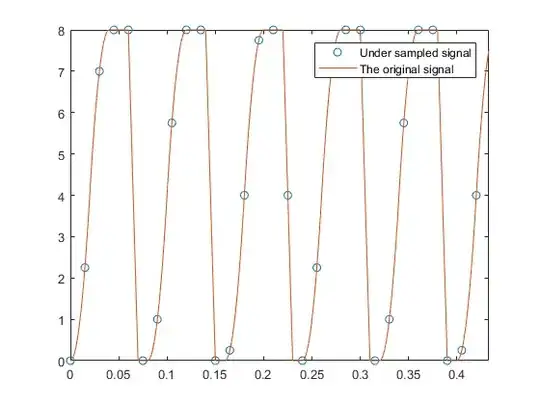
Here is a code to show how to reconstruct the original signal from under-sampled signal. The original signal needs 1/100 sampling period to reconstruct its unique pattern (although its fundamental frequency is 8/100). By sampling with 1.5/100 sec sampling period, the original signal's pattern is reconstructed almost perfectly with reconstruction sampling period of 0.5/100. (In shortly, 0.5/100 sampling period is made from 1.5/100 sampling period.)
dt = 1/1000;
t = 0:1/1000:1.28-1/1000;
x1 = 10000*t(1:20).^2;
x2 = -10000*(t(21:40)-0.04).^2+8;
x3 = 8*ones(1,20);
x4 = -800*t(61:70)+56;
x5 = zeros(1,10);
x = [x1 x2 x3 x4 x5] ;
x = [x x x x];
x = [x x x x]; % make x to be periodic
dtz = 1.5/100;
tz = 0:dtz:1.28-1/1000;
z = x(1: round(dtz/dt) : end);
figure('Name', 'undersampled signal');
plot(tz,z,'o',t,x,'-')
legend('Under sampled signal', 'The original signal')
figure('Name', 'Reconstructed signal');
plot(t(1:5:160),z(mod((0:31)*11,16)+1), 'o-',t(1:160),x(1:160), '-');
legend('Reconstructed signal', 'The original signal')
- 1
-
This could be made a lot clearer. What technique are you using to reconstruct? Where do the magic numbers in "z(mod((0:31)*11,16)+1)" come from? Also, the fundamental PERIOD is 8/100, not frequency - but what matters for Nyquist is the HIGHEST frequency present. – Selvek Nov 02 '18 at 20:33
If a signal is sampled at rate S, any content with frequency f will be indistinguishable from any other content with frequency NS+f or NS-f for some integer N.
Whether a given sample rate is adequate will depend upon whether there exist two frequencies whose content would need to be distinguished, but cannot.
If one is e.g. only concerned about signals in the range 700-800Hz, the input will be devoid of content below 300Hz or above 1200, and the presence of other signals will not cause clipping, a 1000Hz sample rate would be adequate without any pre-filtering, despite the presence of content whose total bandwidth is 900Hz. Content in the range 300Hz-700Hz would be indistinguishable from content in the range 800Hz-1200Hz, but if one doesn't care about any such content that wouldn't matter.
- 45,939
- 2
- 84
- 143