Just complementing the well presented @SuperGeo answer. I think it is important to clarify two points here, which can be cause for confusion:
1. The use of the bilateral Laplace Transform rather than the unilateral one (most used in control systems, when \$t \geq 0\$).
In the latter case, the temporal response must include a multiplication by the unit step function \$1(t)\$.
2. The choice of a not strictly proper transfer function as example. In this case, the step response include discontinuities at origin (\$t=0\$).
When degree of the numerator is equal to the degree of the denominator, the step response presents a step \$1(t)\$ at origin (for the impulse response, there is a impulse \$\delta (t)\$ at origin). So, there will be a direct path between input and output.
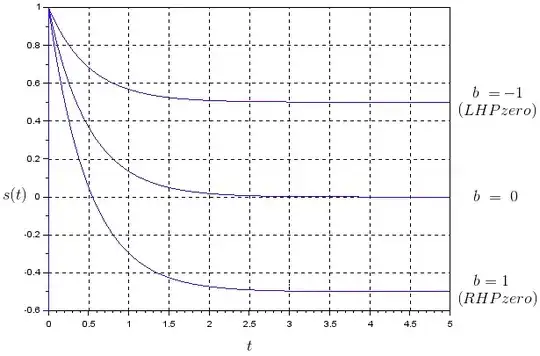
Generically, a first order system like the one below, has a unit step response \$s(t)\$:
$$G(s) = \frac{s-b}{s+a}$$
$$ s(t) = \left [-b/a + \left(1+b/a\right)e^{-at} \right ]1(t) $$
For \$b > 0\$ (RHP zero) there's a change of direction with respect to the value at \$t=0\$ as \$t \rightarrow \infty \$ (as mentioned by @SuperGeo). When \$b = 0\$, the system is classic high-pass filter. For a fixed "a", the quantity "b" on RHP zero just will define the final value of \$s(t)\$. See the plot below for \$a = 2\$:
The examples most frequently presented in the literature for RHP zero behavior are concerned with strictly proper transfer functions and underdamped case (for order 2 or higher). Example:
