2

I am trying to analyse the basic circuit of a dimmer. I don't have much experience in AC circuits, so I am not sure how do I need to proceed. My circuit is the next:enter image description here

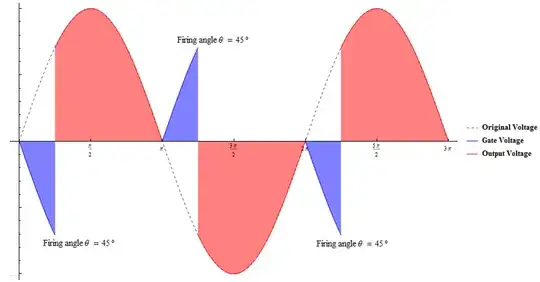
I have something like this:

v

I have found some interesting relationships. Like the output vrms based on the firing angle θ:

Using:

$$ V_{rms} = \sqrt{ \frac{1}{T} \int_0^T v^2(t) dt } $$ we obtain:

$$ V_{rms} = \sqrt{ \frac{1}{ \pi } [ \int_0^{ \theta } 0 d(\omega t) + \int_{\theta}^{ \pi} Sin^2(\omega t) d(\omega t) ] } = \sqrt{ \frac{ V_{max}^2 }{ \pi} \int_{\theta}^{ \pi} \frac{1}{2} [1-Cos(2 \omega t) d(\omega t)]} = \sqrt{ \frac{V_{max}^2}{2 \pi} (\omega t-\frac{Sin(2 \omega t)}{2} ) \Big|_{\theta}^{\pi}} = \sqrt{ \frac{V_{max}^2}{2 \pi} [ \pi-\frac{1}{2}Sin(2 \pi) - ( \theta - \frac{1}{2}Sin(2 \theta) ) ]} = \sqrt{ \frac{V_{max}^2}{2 \pi} ( \pi \theta + \frac{Sin(2 \theta)}{2} ) } = V_{max} \sqrt{ \frac{1}{2} - \frac{\theta}{2 \pi} + \frac{Sin(2 \theta)}{4 \pi} } $$

But I don't know how to obtain the phase angle based on the values of the resistance, the capacitance and the load

Dau
  • 515
  • 8
  • 23
  • 1
    The cap charges from the sinusoidal voltage towards the diac trigger voltage but there is some residual voltage left over from the previous cycle, and much more if it didn't trigger (causing the so-called snap-on effect). You can probably approximate the capacitor voltage as a volt or two of the opposite polarity when the triac did trigger in the previous half cycle. – Spehro Pefhany Dec 11 '16 at 10:32
  • Could you provide a reference, maybe a link?, about the so-called Snap-On Effect, because I am unable to find information about this effect – Dau Aug 15 '19 at 23:59
  • https://electronics.stackexchange.com/questions/429658/questions-regarding-eliminating-hysteresis-in-ac-dimmer – Spehro Pefhany Aug 16 '19 at 00:02

1 Answers1

4

Solution is all but trivial.

A rather good starting point would be doing the following assumptions valid for a resistive load:

1)Each cycle will start with C1 fully discharged and open TRIAC U2.

2)Load resistance is much lower than R3+RV1, hence you will have full half sine mains voltage across TRIAC.

3)DIAC is open circuit untill its breakover voltage VBO (approx 30V) is reached.

4)Now we have to write the transient of C1 being fed with sine voltage via R3+RV1.

5)When vc(t)=VBO TRIAC is fired, capacitor is discharged and your load is being fed.

So KVL to the source, R, C mesh would be $$V_\text{max}\sin\omega t=v_\text{C}(t)+RC\,\frac{\text{d}\,v_\text{C}(t)}{\text{dt}}$$ the usual first order ODE to be solved in \$v_\text{C}(0)=0\$ boundary (or more generally some initial voltage as per Spehro's comment).

This is known to have solution sum of its general \$\breve{v}_\text{C}(t)=A\,\text{e}^{-t/\tau}\quad\tau=RC\$

and particular one \$\hat{v}_\text{C}(t)=\frac{V_\text{max}}{\sqrt{1+\omega^2\tau^2}}\sin\left(\omega t- \arctan(\omega\, \tau)\,\right)\$

Combining them in the above constraint and applying a little trigo gives

$$v_\text{C}(t)=\frac{V_\text{max}}{\sqrt{1+\omega^2\tau^2}}\sin\left(\omega t- \arctan(\omega\, \tau)\,\right)+\frac{V_\text{max}\,\omega\, \tau}{1+\omega^2\tau^2}\text{e}^{-t/\tau}$$

which equated to DIAC break over would give TRIAC on time.

$$\frac{V_\text{BO}}{V_\text{max}}=\frac{\sin(\omega\, t_\text{on}- \arctan(\omega\, \tau)\,)}{\sqrt{1+\omega^2\tau^2}}+\frac{\omega\,\tau\,\text{e}^{-t_\text{on}/\tau}}{1+\omega^2\tau^2}$$

What we really understand from the above is that's indeed job for a numeric solutor.

Edit: one sign fixed upon @Delfin suggestion.

carloc
  • 3,174
  • 1
  • 16
  • 18
  • How did you solve the differential equation? Using: $$ y = e^{-\int a(x) dx}[ \int b(x) e^{\int a(x) dx}dx +c ] $$ I obtain the next: $$ v_c = -\frac{v_{max} \tau ^2 \omega cos[t \omega]}{1+\tau ^2 \omega ^2} + \frac{v_{max} \tau sin( \omega t)}{1+\tau^2 \omega^2} + C e^{\frac{-t}{\tau}}$$ – Dau Dec 11 '16 at 23:29
  • I am trying to see if I can get the same result as yours: $$ \frac{V_{max}}{\sqrt{1+\omega^2 \tau^2}} sin(\omega t + tan^{-1}(\omega \tau)) = \frac{V_{max}}{\sqrt{1+\omega^2 \tau^2}}[sin(\omega t) \frac{1}{\sqrt{1+\omega^2 \tau^2}} + \frac{\omega \tau}{\sqrt{1+\omega^2 \tau^2}}cos(\omega t)]= \frac{v_{max}sin{\omega t}}{1+\omega^2 \tau^2}+\frac{v_{max}\omega \tau cos(\omega t)}{1+\omega^2 \tau^2} $$ I am not sure if I am missing something – Dau Dec 11 '16 at 23:29
  • Uhm I didn't *solve* the ODE, I just added the AC steady state (phasors transalted into time) solution, with the general exponential. My is in the form \$\sin(\omega t + \phi)\$ yous in tne \$a\sin(\omega ) + b\cos(\omega t)\$, obviously they are equivalent. You may try to use some trig, like \$sin(\alpha+\beta)=sin\alpha\cos\beta+cos\alpha \sin\beta\$ and you the get some terms like \$\sin(\arctan x)\$ which can be simplified easily with some Pitagora's on the trigonometric circle. – carloc Dec 13 '16 at 07:41
  • What I mean is that when I solve the ODE I get: $$ v_c = \frac{V_{max}}{\sqrt {1+ \omega^2 \tau ^2}} Sen[ \omega t - tan^{-1}{\omega \tau}] + \frac{V_{max} \tau \omega e^{\frac{-t}{\tau}}}{1 + \tau^2 \omega^2} ] $$ instead of $$ v_c = \frac{V_{max}}{\sqrt {1+ \omega^2 \tau ^2}} Sen[ \omega t + tan^{-1}{\omega \tau}] - \frac{V_{max} \tau \omega e^{\frac{-t}{\tau}}}{1 + \tau^2 \omega^2} ] $$ – Dau Dec 15 '16 at 07:32
  • Oh yes you are right, output signal is to be delayed w.r.t. input one, i.e. shifted right, so minus is what we need. Then exp sign also changes to meet v(0) constraint. This kind of reality check should always be done. Sadly I didn't. I'll fix answer. – carloc Dec 15 '16 at 08:11