5

If I'm using modern D-Flip flops and miss the setup time (i.e. my D input changes close to the clock), the danger is that the F/F will go "metastable" and spend some time oscillating.

Standard designs use 2 F/Fs as a synchronizer to get such an asynchronous signal handled properly inside the local clock domain. When reading about this design, I've seen mentioned the fact that the F/Fs are there to ensure that such oscillations of the first F/F will die down by the time the second clock edge stores the incoming signal in the second F/F.

What I'm curious about is if the synchronizing F/F is guaranteed to settle to the input value after the oscillation time. If my asynchronous signal changed from '1' to '0' at the clock edge, will the Q output be a '0' after oscillating? Or should I assume that I could get an extra clock period where my "synchronized" signal is still a '1'?

Adam Haun
  • 21,331
  • 4
  • 50
  • 91
Bill Nace
  • 253
  • 2
  • 6

3 Answers3

7

There is no cure for metastability. Period. End of.

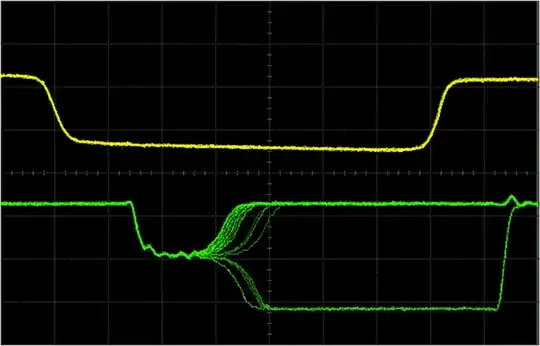
Metastability is a problem in clocked systems when the output of a latch whose input timing constraints have been violated gets read twice. This means either in two different places, or at two different times. With a good signal, these two reads will be identical. With metastability, there's a possibility the two reads will be different.

For instance, the interrupt syncroniser of a uP, 'has an interrupt occurred?' The external interrupt signal is async, so will eventually violate tsu or th. The 'there was an interrupt this cycle' signal gets read in two places. If the program counter thinks there was an interrupt, and the interrupt controller thinks there wasn't, crash!

While there is no cure for metastability, it can be controlled. Any flip flop will be settling with a small time constant, which in a well designed system is small fraction of the clock period. For a particular violation, let's say there is 100% of the output becoming metastable. After 1 time constant, there is a 1/e chance of it still being metastable, 36%. After 10 time constants, it's only 36/million. That may not sound too much, but with a 10Mhz clock, that's 360 failing events per second, far too many. After 20 time constants, it's about 1/billion. One fail every 100 seconds. I wouldn't want to use a PC that crashed that often.

Now we can get any number of time constants by slowing our clock down. However, that impacts system speed. We can buy special 'metastable hard' flip flops, that have much shorter time constants than regular flip flops.

The real win comes when we use two or more flip flops in a row. This increases the signal latency in a system, but it allows us to keep the clock rate up. Do I really care if the external interrupt signal takes two or 3 clock cycles to cause the program jump? Not at all.

So let's say we have a flip flop with 15 time constants per clock cycle. That stands a 0.2/million chance of failure for each metastable event. If I get 1000 interrupts per second from my disk drive, then I might get several crashes a day. Still not very good. Now I cascade two flip flops, and get 30 time constants. I now have 40e-15 chance of failure. This system is unlikely to fail in my lifetime. But wait, say I'm the manufacturer, and have 100 million of these systems in the field. Now I cascade three flip flops, and my expected failure rate drops to 8e-21. I would not expect any failure from any system in my lifetime.

Note the failure rate is still finite, it's not zero. It is however very very unlikely.

Neil_UK
  • 158,152
  • 3
  • 173
  • 387
  • This is a well-written answer to the question of "what is metastabiity and how to solve, ...er.. manage it." But, I was asking about the probability that, after you've "managed" the metastability, that your synchronizer output equals the asynchronous input value. Will you always get a "TRUE" on that synchronized INT input? – Bill Nace Oct 12 '15 at 12:30
  • In the words of the late, great, Patrick Moore, 'we just don't know!' Let's say the async input makes a transition at around the clock edge. In the previous cycle, tsu was met, and the sync agrees with the aysnc, subject to the pipeline delay. In the subsequent cycle, th will be met, and they will also agree. In this cycle, they may agree or disagree, and that's even assuming no metastability. With metastability, you could have two readings of the sync output, one of which agrees, the other doesn't, with the async input. – Neil_UK Oct 12 '15 at 19:11
7

When a flip-flop is metastable it doesn't oscillate. It just gets stuck at an indeterminate level between Vhi and Vlow.

When it finally drops out of the metastable state it could go to either the high or low state.

It's not obvious what you mean by "settle to the input value". Normally you get in to a metastable state by having an input value that is in the middle of a transition when the clock arrives. It's not at either a legal high or low value. So when you say the "input value" neither I nor the flip-flop knows whether you mean the value prior to the transistion or after the transition.

Edit: Here is a scope trace showing the output of a flip-flop going through a metastable state, with the exit from the metastable state taking a random amount of time: enter image description here Picture taken from W. J. Dally, Lecture notes for EE108A, Lecture 13: Metastability and Synchronization Failure (ow When Good Flip-Flops go Bad) 11/9/2005.

The Photon
  • 126,425
  • 3
  • 159
  • 304
  • To avoid having a flip flop go metastable, it is necessary to comply not only with setup and hold times for the data wire, but also with minimum high- and low- times for the clock, and with minimum active times ande minimum release-to-clock times for any asynchronous inputs. A flip flop which is in a metastable state may have its output switch arbitrarily, in any pattern, as long as it continues to be in a metastable state; there's no way of telling whether a single-output flop is in a metastable state unless one has observed that its last "decisive" input stimulus was valid. – supercat Feb 21 '12 at 18:00
  • Note that it is possible "bias" a flip flop such that that it will never output high unless the output is stable high; one could also bias it to never output low unless the output is stable low. One could even design a flip flop with two outputs, one of which would exhibit each behavior. Unfortunately, such abilities are often not as helpful as they would appear. It may seem nice to be able to have a "latch may be metastable" output, but since that signal won't be synchronized with anything, one couldn't use it without latching it somehow (in a latch which might, itself, go metastable). – supercat Feb 21 '12 at 18:10
  • @supercat, while nothing is guaranteed when you use a part outside the operating conditions described in the datasheet, in the real world for real flip-flops (from established commercial CMOS or TTL logic families, or within an FPGA or CPLD) a metastable state will not result in oscillation --- it will involve the output stuck between the high and low levels. – The Photon Feb 21 '12 at 18:29
  • I have never seen a flop where the output would just sit at a stable level which was neither high nor low. While it's true that flops generally can't "oscillate" in the normal sense of the word (since that would require a feedback loop with total phase delay which is a precise multiple of 360 degrees, and in a normal flip flop there are two stages with a phase delay of just over 180 degrees each), it may be possible for the internals of a latch to sit for in a state which downstream logic will sometimes regard as high and sometimes as low. – supercat Feb 21 '12 at 19:23
  • @supercat, It's not stable. It's metastable. Eventually (typically within a few ps or ns put with a very low probability it could take an arbitrarily long amount of time), it decays to a correct logic level. – The Photon Feb 21 '12 at 20:19
  • So you mean the output sits at an intermediate level for some time before yielding a clean high or low. I'll go along with that as a description of the latching element itself; my point was that in many cases one can't directly observe the voltage internal to the latching element, but instead observes some the output of some combinatorial logic which is fed by the latching element, and it's entirely possible that such downstream circuitry might sometimes interpret the signal from the latch as high and sometimes as low. For example, the switching threshold of one gate may be... – supercat Feb 21 '12 at 20:34
  • ...slightly affected by a signal input to an adjoining gate. If input signals never linger near the switching threshold, that wouldn't usually be an issue, but if the output of a metastable latch does sit near the switching threshold, that output could be perceived as switching high and low arbitrarily. – supercat Feb 21 '12 at 20:37
2

When a flip flop goes metastable, nothing is guaranteed about its output state until the next clock event. It is theoretically possible that the mistimed clock might appear to have no effect, but cause the output to switch a second later (in practice, the probability that the circuit will have failed to reach a stable state within time t (implying that the output could spontaneously change some time after that) seconds after the clock drops off exponentially with t, so if hitting the data and clock inputs with some particular timing relationship would have a 1% chance of the output not having stabilized within 1us, there would be a 1/1,000,000 chance of it failing to stabilize within 1ms, and a 1/1,000,000,000,000 chance of it not failing to stabilize within 1sec).

The reason double synchronizers are considered to be effective "armor" against metastability is that metastability on the input to a double synchronizer will only cause metastability on the output if the output of the first flop happens to switch precisely in the "danger" window of the second. Suppose, for example, that one is using a 1MHz clock rate and the flops will switch cleanly except when the data changes in a certain 0.1ns window, in which case the output may change some time later with the probability distribution mentioned above. Even if there would be a 1% chance that the first latch would be inclined to change at some time after 1us, the probability that it will change during the 0.1ns window when the second latch would be "vulnerable" would be much less.

Note that even with a double synchronizer, it's possible for some metastable states to make it to the second latch. If the input to the first latch is deliberately timed to induce such conditions, it may be possible to get metastable states out of the second latch with some predictable regularity (e.g. one in a million latch events or so). Even these, however, won't necessarily result in circuit malfunction if they are used to feed other synchronous logic. Suppose the signal from the second latch feeds two circuits, one of which has 100ns of propagation delay before a latch, and the other has no delay. For the circuit to malfunction, the output from the second latch must switch sometime within the 100ns window before the next clock edge. That's a bigger window than would be required to cause a register to go metastable, but most of the time, even when the second latch goes metastable, it would not happen to result in a switching event within that window.

supercat
  • 45,939
  • 2
  • 84
  • 143