Building a 5-bit Multiplier

Question

I'm currently learning digital logic and have been tasked with building a 5-bit multiplier using only simple gates. I saw it recommended here to use a truth table to help you build the circuit. Unfortunately, for 5x5 multiplication a truth table isn't very realistic as far as I know. Is there another way I could derive a formula that could then be converted to a circuit? Thank you for any help!

Answer 1

To build on Eugene's comment, look at the following schematic:

^{simulate this circuit – Schematic created using CircuitLab}

Note that each bit of the 5-bit value of \$B\$ is used to either gate, or not gate, the 5-bit value of \$A\$ to its associated partial product term. (Numbered as \$PP_0\$ to \$PP_4\$.) \$PP_0\$ is unshifted. \$PP_1\$ is shifted left by 1 bit, so you might think of it as a 6-bit binary value. But I show it as just 5 bits since there's no reason wasting a "0" when all you are doing is a lane-shift.

However, I decided to show that the lowest order bit of \$PP_0\$ is actually the lowest order bit of the result. You can see that in the schematic. At this point, you need to use a half-adder to add the next lowest order bit of \$PP_0\$ (now the lowest bit of the shown 4-bit bus) to the lowest order bit of \$PP_1\$. This will result in \$R_1\$ as the next lowest order result bit. The carry will then ripple over to the next full-adder needed, as you add the remaining 3 bits of \$PP_0\$ to the associated ones of the lane-shifted \$PP_1\$.

Since half adders and full adders are made from simple gates, too, you should be able to generate the entire thing in very simple gates. A lot of them. But the process isn't at all complex. It's just repetitive.

EDIT: For an unsigned \$N\times N\$ multiplier, where \$N\ge 1\$, you will need \$N\times N\$ AND gates to create the \$N\$ partial products for the first stage. This is fast and has a fixed delay. Then you will need \$N-1\$ adder tiers, arranged something like the following 4-bit example (I used 4 bits because 5 bits would have taken too much room on the page.)

^{simulate this circuit}

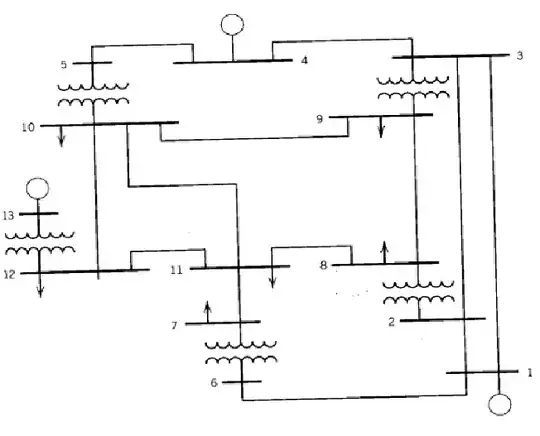
Hopefully, that gets the idea across and you can manage to extend it to 5 bits.