1

How can I model the effect of an (on the order of 1 µH) inductance on the drain of a source follower?

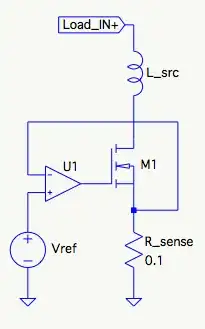
The circuit in question is an electronic load, conceptually this (compensation, gate drive, etc. not shown for clarity):

enter image description here

Motivation

I'm refining the design described in this earlier question of mine. It turns out the stability of the op amp circuit is very sensitive to inductance between the power source under test and the load, typically introduced by the leads used to connect the two.

Based on what adding \$L_{src}\$ to the LTspice simulation does to the loop gain, it looks like the inductance interacts with the net MOSFET drain-to-source capacitance to form an LRC circuit that adds a pair of poles at around 1-2 MHz. The position of the double pole moves depending on the MOSFET and L value used, but their position also depends on the operating conditions because the capacitance of the MOSFET changes significantly with \$V_{DS}\$ (lower \$V_{DS}\$ => higher capacitance).

In any case, I'd like to derive a symbolic expression that characterizes this vertical branch of the circuit from Load_IN+ through the MOSFET to ground, in such a way as to also have symbolic expressions for the poles (and perhaps any zeroes) in terms of L, C, and R. So maybe something of the form:

$$ A \frac{\tau_z s + 1}{s^2 + 2\zeta s + \omega_0^2} $$

What I'm thinking so far

I'm thinking the first step is choosing the right equivalent circuit, which is where I encounter the first conundrum.

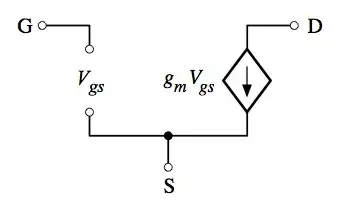
The small signal models I've encountered use a voltage controlled current source; this is the simplest form, neglecting all capacitances and a few other details. The one I would end up using would include at least the parasitic MOSFET capacitances:

enter image description here

My conundrum is a reluctance to place an inductor in series with an ideal current source, which in the ideal case causes an infinite voltage to appear across the inductor on a step current change.

So I'm thinking there are two possible ways to go:

  1. Replace the voltage-controlled current source (VCCS) with a voltage-controlled resistor.

  2. Leave it the way it is, the current source will draw current from the MOSFET capacitances during current transitions, softening the \$di/dt\$ waveform. Also, as long as the transitions are not super fast, the \$di/dt\$ induced voltage across the inductor will remain low enough to keep the MOSFET in its saturation region, and the current source will be an faithful model.

    Just doing some thumbnail calculations, the e-load needs to provide a zero-overshoot (say \$\zeta=0.5\$) 0 - 5 A current step down to at least 3 V source (to test 3.3 V supplies) and 1.5 would be better. And, I was thinking a fixed rise time of about 1 µs (i.e. not building in adjustable slew rate). For a series inductance of 1 µH, that seems like it would mean a \$di/dt\$ of 5 A/µs, producing 5 V across \$L_{src}\$ which would be greater than the DUT supply voltage. So that leads me to the next option:

  3. I need two analyses, one for the usual case of say \$V_{supply} > 10V\$ and another for low voltages.

Can someone with more experience with this sort of thing help me get to the next step?

Community
  • 1
scanny
  • 7,062
  • 5
  • 47
  • 87
  • As soon as you include gate capacitance, you'll have no problem with the vccs producing step current changes. – The Photon Sep 09 '16 at 22:15
  • How about including the MOSFET output resistance in the MOSFET model? – rioraxe Sep 10 '16 at 01:21
  • @rioraxe: The electronic load is a common-drain (source follower) configuration with a 0.1Ω source resistor, so very worst case, \$r_{ds}\$ would be 20Ω, which in parallel with 0.1Ω would be about 0.5% error. So I figure that falls within the tolerance of my current sense resistor and neglected it for this analysis. The model above is just the simplest form I had handy, since the question wasn't about where to put the capacitances and so forth; the model I used for the actual analysis has several more bits on it (and the drain and source swapped as well it turns out :) – scanny Sep 12 '16 at 07:45
  • You expressed a concern for ideal current source in series with an inductor producing infinite voltage due to step current change. Inclusion of r0 in parallel with the current source addresses that, weakly. But for actual small signal analysis, at high frequency, the inclusion of gate capacitance Cgs and especially Cgd is probably much more important anyway. – rioraxe Sep 12 '16 at 20:28
  • @rioraxe: yes, that was the main idea I was missing. Once I realized from The Photon's answer that I would see big voltage transients (i.e. > \$V_{DS}\$ if the capacitance wasn't softening the \$di/dt\$ through the inductor enough it all started to make sense in my head :) Sometimes just a little assurance from someone who's been there before is all it takes :) – scanny Sep 12 '16 at 21:18

1 Answers1

1

Leave it the way it is, but include the gate capacitance and gate resistance in your model also. With these effects included, \$V_{gs}\$ will never change instantaneously, and therefore the VCCS will never produce an instantaneous change in current.

If you still see large voltage transients at the drain node, it likely indicates your circuit should be changed to avoid that problem.

The Photon
  • 126,425
  • 3
  • 159
  • 304