10

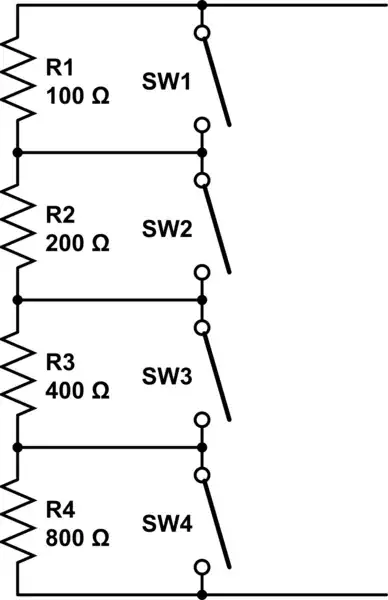
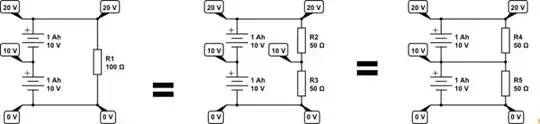
Imagine I have a 10V battery with a capacity of 1Ahrs connected to a 100 Ohm resistor.

I'll get 0.1A (V/R) at a power of 1W (current x voltage) for a total of 10hrs. As a watt is defined as J/s my battery produces 3,600J (1x60x60) in total.

Now, imagine I get a second, identical battery and connect it in series to the first one. I will effectively have a battery of 20V with a capacity of 2Ahrs, all connected to the same 100 Ohm resistor.

I'll get 0.2A at a power of 4W (current x voltage) for a total of 10hrs. This will generate 14,400J (4x60x60).

So, from doubling my energy source I have quadrupled the energy output!

I've obviously made an error somewhere either in my calculations or conceptual understanding, and I would be most grateful to anyone who could set me right.

Thanks!

user122374
  • 129
  • 1
  • 5
  • 30
    *20V with a capacity of 2Ahrs* - wrong. Connecting batteries in series is not adding their capacities. You will get the same 1Ah – Eugene Sh. Aug 31 '16 at 17:52
  • 14
    Connecting two batteries in series doubles their Wh, by virtue of doubling the voltage, but the Ah stays the same. – Neil_UK Aug 31 '16 at 18:01
  • 5
    Imagine you have a leaky bathtub containing 1 liter of water, that is draining at 0.1 liters per hour and will drain for 10 hours before empty. Now place a second, identical leaky bathtub beside it. You effectively have one large bathtub that will drain 0.2 liters per hour for 10 hours. OK, now place the second bathtub *above* the first bathtub, so that it drains into it. What makes this new system suddenly start draining at 0.2 liters per hour out the bottom bathtub? Nothing. You now effectively have a bathtub with 2 liters of water in it, but that doesn't make it drain faster. – Eric Lippert Aug 31 '16 at 21:13
  • 2
    Thanks for the responses. I'm not sure your analogy works here, @EricLippert because the batteries will push out double the current, unlike the two stacked bathtubs. But it appears from the other answers here that it will drain for half as long. – user122374 Aug 31 '16 at 22:42
  • 1
    @user122374 the tubs stacked on top of one another (series) will NOT provide more current – Doktor J Sep 01 '16 at 06:36
  • @DoktorJ Yeah, but the batteries will. – user253751 Sep 01 '16 at 11:58

3 Answers3

44

Congratulations for having the wit to know something was wrong!

schematic

simulate this circuit – Schematic created using CircuitLab

Figure 1. Parallel and series arrangements of batteries will have the same VAh rating.

I will effectively have a battery of 20 V with a capacity of 2 Ah.

That's the error.

  • In parallel they can supply 1 A each for one hour. This is very easy to visualise if you run one for an hour and then replace with the other.
  • In series they both run simultaneously and the same current runs through both of them. They will both discharge at the same rate.

This is one good reason to use Wh (watt-hours) for battery comparison. It makes it much easier to compare battery energy storage when the batteries have different voltages.

In your example you have \$ Capacity = V \cdot Ah = 10 \cdot 1 = 10~Wh \$. With two batteries we have \$ 20~Wh \$ capacity whether in series or parallel.

Our load power is given by \$ P = \frac {V^2}{R} \$.

  • In parallel \$ P = \frac {10^2}{100} = 1~W \$ as you calculated. \$ Runtime = \frac {Wh}{W} = \frac {20}{1} = 20~h \$.
  • In series \$ P = \frac {20^2}{100} = 4~W \$ as you calculated. \$ Runtime = \frac {Wh}{W} = \frac {20}{4} = 5~h \$.

schematic

simulate this circuit

Figure 2. An alternative view may help. (a) Is your original series circuit. (b) is a direct equivalent. Because the mid-point of the 50 Ω resistors is at the same potential as the mid-point of the battery stack it makes no difference if we connect them together as shown in (c). Now we have two 1 Ah circuits each feeding into a 50 Ω load.

Transistor
  • 168,990
  • 12
  • 186
  • 385
14

When you double the batteries, you double the current, and consequently quadruple the power in the resistor. You got all that correct.

However you seem to have missed that by doubling the current, you also halve the runtime of your batteries. So it won't run for 10 hours, but 5. So the total energy is only doubled, not quadrupled.

When you connect batteries in series like this, the charge capacity of the resulting composite battery (typically in mAh) does not change. It doesn't change because each unit of charged moved through the battery must also move through each cell. So adding more cells (or batteries of cells) in series does not increase the total charge that can be moved by the battery in its lifetime, but it does increase the voltage over which that charge can move, which accounts for the extra chemical energy you've added.

Phil Frost
  • 56,804
  • 17
  • 141
  • 262
  • Thanks Phil, the concept you mentioned of how much charge passes through each cell helped understand what's going on. – user122374 Sep 02 '16 at 06:17
7

I'll get 0.2A at a power of 4W (current x voltage) for a total of 10hrs.

Since neither battery can supply 0.2A for 10 hours, and both would need to for this to be true, this is false.

The same current flows through both batteries and that's the same as the current through the load because this is a pure series circuit. So in order to supply 0.2A to the load, each battery needs to be able to supply 0.2A.

Now, imagine I get a second, identical battery and connect it in series to the first one. I will effectively have a battery of 20V with a capacity of 2Ahrs, all connected to the same 100 Ohm resistor.

You don't show how you got 2Ahrs, but that's not correct. Again, both batteries have to supply the full current. Since each battery can supply 1Ah, the two together in series can supply 1Ah because the currents don't add up in a series connection.

David Schwartz
  • 884
  • 5
  • 9
  • I like this answer because it drills down into the "no, not 2Ahrs" question in the most understandable way. – Floris Sep 02 '16 at 12:19