So ive been playing with some Sigma Delta ADCs, for sampling low frequency (<2Khz) AC signals.
The ADC supports a differential input with a full scale value of about +-500mV at its inputs. I have constructed a reference design which consists of an input attenuation network that takes my input voltage, divides it by a factor of about a 1000 which then appears across the ADCs inputs; i also have an anti aliasing filter etc.
To play around with it, i decided to measure a few DC voltages far less than the usual full scale AC input (220v RMS) i would be using normally. What ive noticed is that there is some inherent noise from the ADCs outputs. For example, for an input of 30v DC verified to be stable, i see about 80mV noise (random, +- variations) in the readings. The noise seems to have a fundamental of about 100-200Hz.
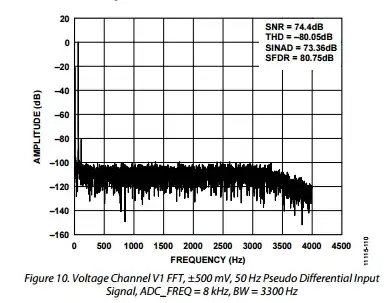
I think i understand concepts such as noise floor, quantization noise, spurs etc so I wanted to see if i could explain this; so i turned to the datasheets performance figures for the ADC and i found this:
I believe this explains my observations; I can see a spur about 80dB down from the reference input, around the noise frequency i observed.
Furthermore, I made a few calculations:
500mV is the full scale reference level shown in the graph, so the spur that is 80dB down, represents 50uV worth of noise at the ADCs input. As i have an attenuation network of about 1000, that translates to an equivalent value of about 50uV * 1000 = 50mV worth of noise in my input voltage. This is close to the 80mV noise figure i observed.
My question is: Is such analysis valid and could explain my observations?
PS: This question is a bit tricky to explain, please comment for additional information
EDIT 1: Here is the ADC that im talking about: datasheet