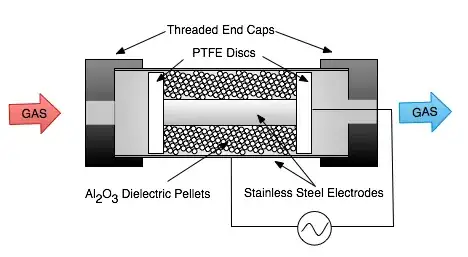
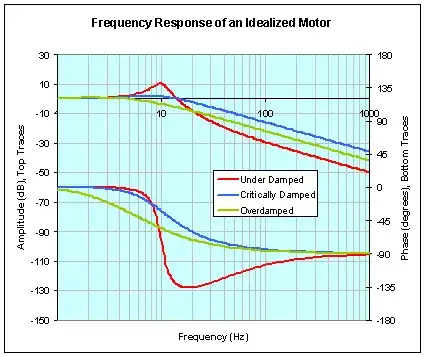
The question assumes there is one damping factor i.e. the transfer function is dominated by a 2nd order system. In practice there could be several interacting 2nd order systems so care has to be taken here.
Assuming it is dominated by a single 2nd order system, this diagram may be useful: -
This picture allows you to calculate \$\zeta\$ by looking at the peak amplitude value in the bode plot. From this you can calculate \$\omega_n\$ using the 2nd formula. Once \$\omega_n\$ is known you can double check the value of Q (1/2\$\zeta\$) because, for a 2nd order filter like this Q IS the magnitude of the amplitude response at \$\omega_n\$.
Here's the bigger picture showing how the bode plot and pole zero diagram are related: -