0

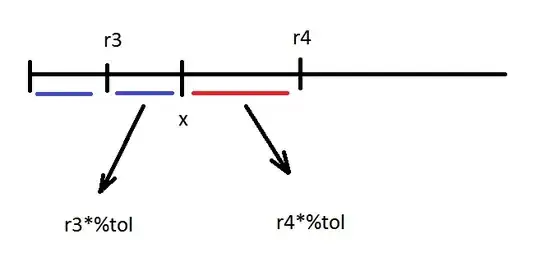
enter image description here

I'm trying to calculate E12 resistor series myself.

Above is an illustration of the idea where such equation can be written:

x = r3 + r3 * %tol = r4 - r4 * %tol

form that we can derive:

r4 = r3* [(1 + %tol)/(1 - %tol)]

hence in generalized form we can write (%tol = 0.1 for E12 series);

r(i+1) = ri* [(1 + %tol)/(1 - %tol)]

But when I iterate the above formula in a for loop I obtain the following results for the first resistor values:

1.0000 1.2222 1.4938 1.8258 2.2315 2.7274 3.3335 4.0743 4.9797 6.0863 7.4388

Then I take [(1 + %tol)/(1 - %tol)] = 1.2 rounded value instead of 1.222222 and write the formula as:

r(i+1) = r(i)*1.2

But again when I iterate the above formula in a for loop I obtain the following results for the first resistor values:

1.0000 1.2000 1.4400 1.7280 2.0736 2.4883 2.9860 3.5832 4.2998 5.1598 6.1917

But the real values for E12 should be as:

1.0, 1.2, 1.5, 1.8, 2.2, 2.7, 3.3, 3.9, 4.7, 5.6, 6.8

What am I doing wrong here?

user16307
  • 11,802
  • 51
  • 173
  • 312
  • 1
    "What am I doing wrong here?" assuming that the E12 series follows your formula? – PlasmaHH May 25 '16 at 09:11
  • I took E12 series with tolerance %10 – user16307 May 25 '16 at 09:15
  • tolerances have little to do with calculating the numbers, they are a result of the spacing. They are based on renard series. – PlasmaHH May 25 '16 at 09:19
  • I see tolerances is the consequence not the motivation here? i should find out why they use renard series and how to formulate it – user16307 May 25 '16 at 09:24
  • The choice of the exact series (6/12/24) seems to play a role in getting convenient tolerances(20/10/5). You can also see that the tolerances do not determine the values by taking the values and determining the percent distance to the adjacent values, which are all over the place. – PlasmaHH May 25 '16 at 09:27
  • can you write this with an illustration as an answer so i can accept and see more clearly – user16307 May 25 '16 at 09:29
  • I could not do this any better than the wikipedia article, which even has a nice graph for E12 – PlasmaHH May 25 '16 at 09:33
  • Additional info / related question: http://electronics.stackexchange.com/questions/67975/what-is-the-reason-that-the-value-47-is-so-popular-in-electrical-engineering – zebonaut May 25 '16 at 09:59
  • Try this: http://electronics.stackexchange.com/questions/67975/what-is-the-reason-that-the-value-47-is-so-popular-in-electrical-engineering/67984#67984 – Andy aka May 25 '16 at 11:04

3 Answers3

2

The general formula for one decade of all Exx resistor series (xx = 3*2^m, for m = 0 to 6)

Rn ~ 10^(n/xx) for n from 0 to xx-1

As you will realise, ~ means approximately equal, and not even always correctly rounded! The general intention was to get all the resistors into a nice geometrical series, and then adjust the numbers to some nice, low number of significant digits, and have successive series to be sub/supersets of each other to improve stock logistics. Unfortunately this means that the resulting numbers can be quite unequally spaced. The most irritating (to me) place that this happens is in the E24 series, where part of the sequence runs 1.3, 1.5, 1.6, 1.8.

As the series become finer, the number of significant figures increases, which means that not all series are sub/super the next one.

E3, E6, E12 are all subsets of E24, which use two significant figures. E48 and E96 are subsets of E192, which use three.

While finer series tend to have smaller tolerances, the tolerance is really an economic thing, you pay for as much as you need.

Neil_UK
  • 158,152
  • 3
  • 173
  • 387
  • can you also add the definitions of m n xx in your answer? thnx – user16307 May 25 '16 at 15:06
  • @user16307 I'm not sure what you're asking, the definitions are there in my answer. Perhaps you would prefer words to symbols? xx equals three times (two raised to the power of m), where m takes values zero through to six (OK, I should have said **integer values** in my answer, R(n) is approximately equal to ten raised to the power of (n divided by xx), where n takes **integer values** between zero and (xx takeaway one). Does that help? So xx ends up taking values 3, 6, 12 ... 192. – Neil_UK May 25 '16 at 19:43
  • you wrote "where n takes integer values" is this a definition of n? is this the number of "what"? what does n represent? same with m. can you relate these parameters what they point to? – user16307 May 26 '16 at 08:58
  • @user16307 I haven't a clue how I can be more explicit about n, than the phrase 'n takes integer values between 0 and (xx-1)', perhaps examples would help. When xx is 3, for the E3 series, n then takes values 0, 1 and 2. When xx is 24, for the E24 series, n takes values 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and 23. I could give the values that n takes for the E192 series, but I'm hoping that you've got the general picture by now. Similarly m goes from 0 to 6, and for m=0 gives us the E3 series, m=4 is E48, and m=6 gives us the E192 series. – Neil_UK May 26 '16 at 12:37
1

I've calculated the values for E12, 24, 48, 92, 196 using geometric series. I found:

  • 12 differences for E12
  • 21 differences for E24
  • 0 differences for E48
  • 0 differences for E96
  • 1 difference for E192

The difference for E192: officially the 185th value is: 9.20, my calculation results in 9.19.

The calculation is: perl -e 'printf("%.2f\n", (10**(185/192)))'

The decimal value for 10**(185/192) is 9.19478686318879.

I'm wondering what rounding method was used to calculate the official values...

Bernhard Wagner
  • 111
  • 2
0

The E series of resistor values indeed don't exactly follow what you would expect from taking a geometric series and rounding it to the appropriate number of decimals.

There is some speculation on this on the Wikipedia talk page incluing a reverse engineered algorithm for generating the numbers but noone seems to have found a definitive answer for why the numbers are the way they are https://en.wikipedia.org/wiki/Talk:Preferred_number/archive1#Resistor_series

Peter Green
  • 21,158
  • 1
  • 38
  • 76
  • so the motivation to write a formula is not how I structured? i thought the idea is each resistor values neighborhood were set due to tolerances as in my question. – user16307 May 25 '16 at 09:18
  • Since the dawn of time, the explanation I heard was "renard series with some greybeard changes and/or mistakes". – PlasmaHH May 25 '16 at 09:20
  • @user16307 not exactly, the idea is to have 12 evenly spaced values on a logarithmic scale per decade. Ideally then each value should be separated by a factor of 10^(1/12) or about 1.211. Keeping only two significant figures and making some adjustments for rounding (and who knows what else), we have the E12 values. Then using the formula you provide, it's clear the the tolerance is roughly 10%. – jonvw May 25 '16 at 11:25