-1

I made a contact debouncing circuit using a capacitor. The main idea was to charge the capacitor, so that the bouncing on the signal would be "smoothed out".

enter image description here

It works, but It's been a while since I last looked at it, and I don't understand exactly why/how the capacitor charges and discharges slowly when the contact is switched ON/OFF.

Is there no charge on the capacitor, when the switch is ON and there's 5 V on both sides? And if so, then why does the voltage drop slowly, when the contact is switched OFF?

Circuit simulation: http://goo.gl/itgLb8

ASM_JOE
  • 1
  • 2
  • 1) this circuit makes little sense and looks weird 2) debouncing **is** possible using a resistor and a capacitor, these make a filter, filtering out rapid changes resulting from contact bounce 3) in practice most switches are connected to a microcontroller and some software running on it takes care of contact bounce. 4) you might want to Google on this subject and see how others solve this and try to understand how and why things are done like that. – Bimpelrekkie May 23 '16 at 08:27
  • You may want to read [this question](http://electronics.stackexchange.com/questions/28251/rules-and-guidelines-for-drawing-good-schematics) about drawing schematics. – Dmitry Grigoryev May 23 '16 at 08:35

2 Answers2

1

This is only a reliable debounce circuit if the gate is a Schmitt trigger type.

The RC forms a low pass filter with a time constant:

\$\tau=RC=10\mu F \cdot 1K\Omega = 10ms\$

(It's actually 1.22K when discharging and 1K when charging, but let's ignore that minor difference).

That's the time to charge from 0 to 63% of 5V (3.2V) or from 5V down to 1.8V. If we assume a couple 74HC14 ST inverters in series for the gate, the positive-going threshold voltage will typically be around 2.6V and the negative-going around 1.6V with a 5V supply (see table 10 for typical values at 25°C and 4.5V Vcc) and multiply by 5/4.5), so the calculated \$\tau\$ is reasonably close to the times to reach thresholds (tolerances on the C especially are usually pretty loose).

Typical bounce times for a switch might be 5ms maximum (check the data sheet) so a 10ms time constant does a reasonable job without slowing the switch action too much.

The reason why the Schmitt trigger is necessary is that with it you have ~1V typically of noise immunity at all times. With just an ordinary gate there is a time window as the voltage (slowly, from the point of view of a gate) slides up or down through the transition voltage, and any kind of noise (say switching noise on the power supply or on the wires to the switch) can cause the output to bobble back and forth. The noise immunity approaches zero as you pass through the transition.

If you need debounce (for example, for the clock input of a counter) this can cause false counts.

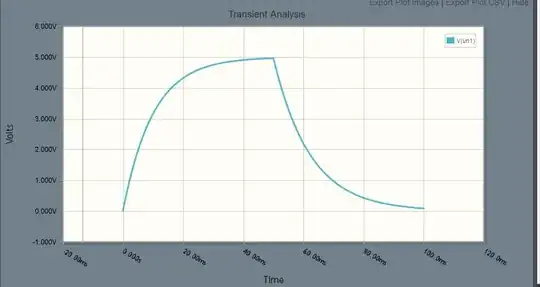
Here is what the voltage input to your ST looks like if the switch is closed at t=0 and opened at t=50ms. If the switch chatters back and forth a bit on a scale of milliseconds or less it won't change instantly between the two hysteresis points of the ST so the switch is debounced effectively.

enter image description here

Spehro Pefhany
  • 376,485
  • 21
  • 320
  • 842
  • The input goes into a ST on a microcontroller. I should have said that. I do, however still not understand how/when the capacitor charges ? And why is there 5 V on the outputwire? Doesn't the resistor reduce the voltage? – ASM_JOE May 23 '16 at 11:47
  • When the switch is open it discharges to ground through 10K + 220. When the switch is closed it charges towards +5 through 10K (the 220 is just across the +5 to 0V and does nothing but get warm). It might be easier to visualize if you move the bottom capacitor connection to ground rather than +5 (it makes no difference except when it is first powered up). After a few tens of milliseconds the output voltage is either +5 or 0V (close enough anyway) assuming there is minimal loading. – Spehro Pefhany May 23 '16 at 12:33
  • Wait there do exist Schmitt trigger buffers right? – Bradman175 May 23 '16 at 13:49
  • So the capacitor is charged when the switch is open even though the bottom capacitor connection is connected to 5 V? How can the capacitor charge, if there's 5 V on the bottom pin and 5 V (through a resistor) on the top pin? Should'n there be a difference in those two voltages for it to charge? – ASM_JOE May 23 '16 at 13:53
  • @ASM_JOE It's not really important whether the capacitor charges or discharges - it moves toward the voltage connected through the resistor, and the curve looks the same whether the other side of the capacitor is connected to 0V, 5V or 1000VDC, provided the initial voltage is the same. – Spehro Pefhany May 23 '16 at 14:45
  • 1
    I think understand all of it now. I should have just connected the bottom pin on the capacitor to GND. That would had made the circuit easier to understand. I owe you a big thank you! – ASM_JOE May 23 '16 at 16:16
0

The capacitor charging curve depends on his capacity (10uf here) and the applied voltage. If you think it's too slow, it's because the capacity is too important. You can approximate the charging time. It's about $$ 3*R*C \simeq 30ms$$ (95% of final charge)

To calculate the charge the formula is $$ I = C \frac{dV}{dt} $$ If the voltage is null (5v on both side), there is no current. No current means charges not moving. So if there is 5v on both side of the capacitor, the charge remain constant. We can't say if is empty or not, it depends on the previuous state.

I hope I help you?

Nicolas Perraut
  • 101
  • 2
  • Thank you very much So if the contact is first OFF and the capacitor is charged, the charge will still be there after the contact has been switched on and off? So it works like this: 1. The contact is OFF and the capacitor is charged 2. The contact is ON, the capacitors charge remain, and the charge is NULL 3. The contact is OFF, and the capacitor will disscharge? – ASM_JOE May 23 '16 at 08:49