2

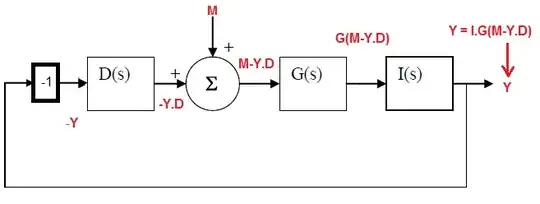
I have a question regarding a control loop system which is subject to disturbance, unfortunately I missed a couple of lectures on the subject and now am scratching my head as to how to do it. The loop is shown below.

enter image description here

\$D(s)=\frac{K}{s+10},\$ \$M_p(s)=\frac{M_o}{s},\$ \$G(s)=\frac{s+3}{s^2+4s+5},\$ \$I(s)=\frac{1}{s}\$

\$K_t\$ isn't used for now so that can be ignored. \$M_p\$ is a step input disturbance.

Anyway, the question in hand is asking for the steady state error assuming the system to be stable, and I am simply struggling with getting the initial T.F. in order to get this.
It is given that I need to determine \$\frac{\theta(s)}{M_p(s)}\$ and furthermore am given that this is: $$\frac{(s+3)(s+10)}{s(s+10)(s^2+4s+5)+K(s+3)}$$

But I baffled as to how to get to this result, any ideas?
After this I know what to do but I just want to know how to get to this stage in the first place.

Community
  • 1
MrPhooky
  • 2,168
  • 8
  • 24
  • 55
  • 1
    Forward path is G(s)I(s), feedback path is D(s). Assume \$\theta_{ref}=0\$. To see this, re-draw the block diagram with the input signal of interest, \$M_p\$, on the left. – Chu Apr 28 '16 at 09:31
  • \$\theta=G\cdot I(M_p+D\cdot (\theta_{ref}-\theta ))\$, can you take it from here? – Vladimir Cravero Apr 28 '16 at 09:55
  • @VladimirCravero Yeah I can get that I struggle to get \$\frac{\theta}{M_p}\$ on its own though... – MrPhooky Apr 28 '16 at 10:10
  • 2
    Hint 2: \$\theta\cdot(1+D\cdot G\cdot I)=M_p\cdot G\cdot I\$, using \$\theta_{ref}=0\$. If you can't get it from here you need to exercise on algebra, not control systems. – Vladimir Cravero Apr 28 '16 at 10:20
  • Then plug in all the other formula! – Andy aka Apr 28 '16 at 10:24
  • @VladimirCravero Haha, thanks, I manage to forget my basic algebra sometimes... Thanks for the shove in the right direction! – MrPhooky Apr 28 '16 at 10:36

1 Answers1

2

Just redraw the diagram like this: -

enter image description here

I've used Y instead of theta for my own convenience.

You get Y = I.G(M - Y.D) which reduces to \$\dfrac{Y}{M} = \dfrac{1}{\frac{1}{G.I} + D}\$

I can see that if you plug the expressions for G, I and D in you get the correct answer.

Andy aka
  • 434,556
  • 28
  • 351
  • 777