Common drain / source follower stage circuit analysis

Question

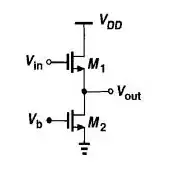
I have been recently working on different types of MOS amplifiers and the following are my main doubts,

1. When we have a high gain stage such as the common source stage we use the output of this stage as an input to a common drain stage. What makes the common drain stage so special? I know that they charge capacitors in a much quicker rate (slew rate) compared to the common source stage but is there an intuitive way to understand what makes the common drain stage good for this?

2. In terms of slew rate is the push pull stage (with the distortion effect corrected) a better option compared to the common drain stage as the final output stage?

Common drain stage <----------> Push-Pull stage

Answer 1

I have personally never understood the appeal of 2 stage amplifier in the classical AB sense, and for that reason I never make them that way, but every single textbook has a 2 stage amplifier. Regarding the output stage in the classic sense, I believe the reason is that you want enough output resistance for the feedback compensation to keep from ringing. I use a cross coupled output stage that is similar to LMC6484. You can get that output stage from the datasheet.

Regarding 1, the common drain stage is nice because it is biased to be at the edge of subthreshold so it have a very good linear behavior. The "charging" faster part is just due to the fact there's less total capacitance. The band diagram looks like this (pulled from one of my lectures):

If you make the assumption that the devices are large so the threshold currents match, the result is: $$ I_{th}e^\left(\frac{\Phi_{sc1}}{U_t}\right)=I_{th}e^\left(\frac{\Phi_{sc2}}{U_t}\right) $$ This then can be modified with voltages based on the schematic above: $$ I_{th}e^\left(\frac{\kappa V_{bias} -0}{U_t}\right)=I_{th}e^\left(\frac{\kappa V_{in} -V_{out}}{U_t}\right) $$ You can then push through the math and you get: $$\Delta V_{out} = \kappa V_{in} -\kappa V_{bias}$$