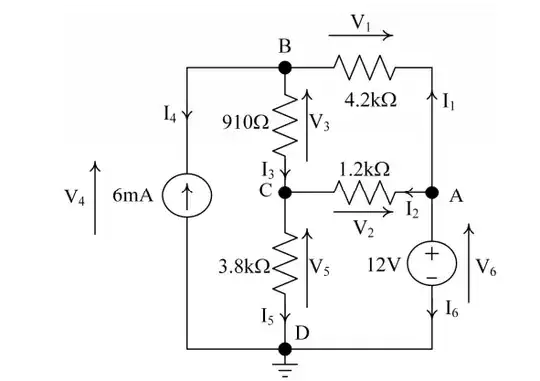
The rules for nodal analysis is that current flows from the higher potential node to the lower potential node, with the mathematical equation being:
\$I = \frac{Vhigher-Vlower}R\$
However, how do we determine which node has the higher potential. Ground node against any other node is easy because ground is always \$0v\$, but for other nodes (say Node A to Node B), how do we determine which is higher.
Edit: In the current question I am doing, I am given the arrows for the direction of the voltage, along with the direction of the current (This is just a practice question). So I am assuming it is related to one of these two but which?
So far I have gotten the KVL and KCL, along with \$VoltageA = 6v, VoltageD = 0v\$.
I have no idea how to proceed from here