How does division occur in our computers?

Question

How does division occur inside digital computers? What is the algorithm for it?

I have searched hard in google but haven't got satisfactory results. Please provide a very clear algorithm/flowchart for division algorithm with a sample illustration.

Answer 1

Division algorithms in digital designs can be divided into two main categories. Slow division and fast division.

I suggest you read up on how binary addition and subtraction work if you are not yet familiar with these concepts.

Slow Division

The simplest slow methods all work in the following way: Subtract the denominator from the numerator. Do this recursively with the result of each subtraction until the remainder is less than the denominator. The amount of iterations is the integer quotient, and the amount left over is the remainder.

Example:

7/3:

1. $$7-3=4$$
2. $$4-3=1$$
3. $$1 < 3$$

Thus the answer is 2 with a remainder of 1. To make this answer a bit more relevant, here is some background. Binary subtraction via addition of the negative is performed e.g.: 7 - 3 = 7 + (-3). This is accomplished by using its two's complement. Each binary number is added using a series of full adders:

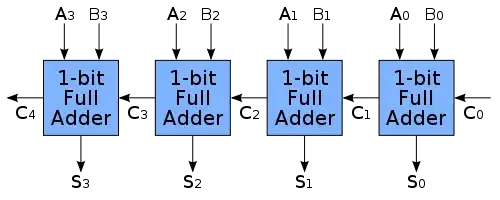
Where each 1-bit full adder gets implemented as follows:

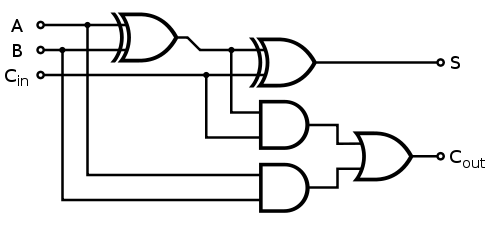
Fast Division

While the slower method of division is easy to understand, it requires repetitive iterations. There exist various "fast" algorithms, but they all rely on estimation.

Consider the Goldschmidt method:

I'll make use of the following: $$Q = \frac{N}{D}$$

This method works as follows:

1. Multiply N and D with a fraction F in such a way that D approaches 1.
2. As D approaches 1, N approaches Q

This method uses binary multiplication via iterative addition, which is also used in modern AMD CPUs.

Answer 2

Hardware for floating point division is part of a logic unit that also does multiplication; there is a multiplier hardware module available. Floating point numbers, say A and B, are divided (forming A/B) by

1. decomposing the floating point numbers into sign (+1 or -1), mantissa ("a" and "b", and (binary integer type) exponents
2. the sign of the result is (+1) iff both signs are the same, else (-1)
3. exponents are subtracted (exponent of B subtracted from exponent of A) to form the exponent of the result

4. mantissas (the binary digits of the numbers) are a fixed-point binary number between 1/2 and 1; that means that the first digit after the binary point is '1', followed by zeroes and ones... as a first step, a lookup table finds the reciprocal accurate to six bits (there are only 32 possibilities, it's a small table)

5. to begin to compute a/b, do two multiplications $$ {a \over b} = {{a * reciprocal(b)}\over b * reciprocal(b)} $$ and note that six-bit accuracy implies that the denominator of the result is very near 1 (to five or more binary places).

6. Now note that for very-near-one denominators, 'd', we can see that defining$$ d == 1 +\epsilon $$ $$ d * (2-d) = ( 1+ \epsilon) \times (1-\epsilon) = 1 - \epsilon ^2 $$ This implies that our five-bit accurate 'one' in the denominator will become ten-bit accurate after one more pair of multiplications, twenty-bit accurate after two, and forty-bit accurate after three. Do as many iterations of multiplying numerator and denominator by (2 - denominator) as your result precision requires.
7. The numerator, now that the denominator is exactly '1', is the mantissa of the result, and can be combined with the previously computed sign and exponent.
8. IEEE floating point allows some exceptions (denormalized numbers, NAN; those have to be handled by other logical operations.

Interestingly, the old Pentium divide bug (very newsworthy in 1994) was caused by a printing error that made faulty reciprocal-table values for step (4). An early paper, "A Division Method Using a Parallel Multplier", Domenico Ferrari, IEEE Trans. Electron. Comput. EC-16/224-228 (1967), describes the method, as does "The IBM System/360 Model 91: Floating-Point Execution Unit" IBM J. Res. Dev. 11: 34-53 (1967).

Answer 3

There are very different methods for division, depending on the numbers to be handled. For integers, the shift-and-subtract method given by others will work fine. For floating point numbers, however, it may be quicker to first compute the reciprocal of the denominator and then multiply that times your numerator.

Computation of the reciprocal of the denominator is not so bad; it is done by refining successive approximations. Let g be your guess for 1/d. For an improved guess, use g'=g(2-gd). This converges quadratically, so you double the digits of precision on each improvement.

Example: compute the reciprocal of 3.5.

Your initial guess is 0.3. You compute 0.3 * 3.5 = 1.15. Your adjusted guess is 0.3 * (2 - 1.15) = 0.285. Already pretty close! Repeat the process, and you get 0.2857125, and a third try gets 0.2857142857.

There are some shortcuts. In floating point, you can extract powers of ten or powers of two, depending on the number base of your machine. And, for speed at the expense of greater memory use, you can use a pre-computed table for numbers in the range of 1 to b (where b is your number base) to get a guess that is immediately close to the required reciprocal and save one or two refinement steps.

Keep in mind that, as with multiplication and Kolmogorov's 1960 embarrassment by his student Anatoly Karatsuba, you never know when a faster or better method will be found. Never surrender your curiosity.

Answer 4

Computers don't do iterative addition to multiply numbers - it would be really slow. In stead, there are some fast multiplication algorithms. Check out: http://en.wikipedia.org/wiki/Karatsuba_algorithm

Answer 5

All credits goes to anand kumar(the author of this book)