Effect of battery internal resistance on its energy efficiency

Question

I am trying to calculate Li-ion/LiPo battery's energy efficiency based on its internal resistance (as far as I see from scientific papers, the battery's internal resistance rises with its ageing, meaning that the efficiency must decrease).

Discharging: I use the most basic equivalent circuit and load:

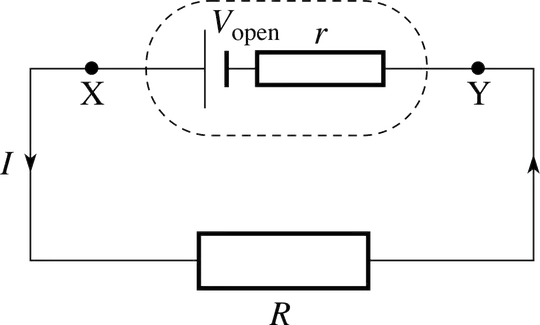
If I assume that the current is constant (the way they describe it here), then I get:

ef = (Vopen-Ir)/Vopen (probably I should integrate this by time)

(I have reduced the current and the charging time in both parts of the fraction).

By the same method, the charging efficiency will be: V/(V+Ir)

Therefore if we want to calculate the round-trip efficiency (output power/input power), it will be the multiplication of the two, giving (V-Ir)/(V+Ir)

1. Am I doing this right? Does it mean that for every charging/discharging current, the efficiency is going to be different?

2. I guess there are other factor affecting the energy efficiency, although I haven't quite found any formulas. How significant are they in comparison to internal resistance?

Answer 1

Modeling battery charge and discharge processes is a very intricate science. There are many models to estimate the behavior of a battery. Using a internal series resistance can be useful to estimate a rough state of charge as well as the power efficiency when dis-(charging). This model is not very exact thus calculating the charge efficiency the error will integrate over time as well leading to a large total error.

To understand the basic behavior of batteries take a look at the Peukert Effect (aka. rate-capacity effect) and the Recovery Effect. In a nutshell:
The Peukert Effect describes that one can get more charge out of a battery if discharged with a low (constant) current. The Recovery Effect says that in periods of low/no discharge currents the reduced "useable" charge due to high current loads gets partially replenished. The reasons for both are the chemical processes in the battery.
If you want a very accurate model of a battery for your calculations look for electrochemical models (most notable DualFoil, based on work of Doyle et al.). For easier use with good accuracy the (analytic) Kinetic Barrier Model comes to mind. Also there are more sophisticated electric models filling the gap between the two aforementioned.

Edit: Calculating the Peukert constant

Given the capacities \$Q\$ and their respective run-times \$T\$ for two constant discharge currents \$I_a\$ and \$I_b\$, the Peukert constant \$k_P\$ can be calculated as
\$k_P = \frac{ln\frac{T_a}{T_b}}{ln\frac{Q_b}{Q_a}+ln\frac{T_a}{T_b}}\$.
The required values can be derived from the batteries specifications or actual measurements.

Answer 2

1. Am I doing this right? Does it mean that for every charging/discharging current, the efficiency is going to be different?

The basic formula is correct. however internal resistance also varies as the battery charges/discharges and with temperature, so with a fixed resistance value it will only be accurate when cycling the battery at low current and over a fraction of its full capacity (and that is assuming you have an accurate measurement of internal resistance in that range).

Theoretically each cycle will have lower efficiency than the previous one, but since the battery degrades slowly the effect is very small.

2. I guess there are other factor affecting the energy efficiency, although I haven't quite found any formulas. How significant are they in comparison to internal resistance?

Resistance is the only electrical parameter what causes power loss, so if your resistance value is accurate then no other factors need be considered. However in practice that resistance is affected by several factors such as temperature, current, and state of charge. Voltage also varies with charge state, so you need an accurate voltage vs charge curve.

In practice, if the battery doesn't heat up significantly you can assume that the charge/discharge cycle is close to 100% efficient. Charging is normally done at relatively low current so this is usually true. Discharge current may be much higher, and then you will see more heating and higher temperatures. Internal resistance increases as the battery ages, so an old battery will get hotter - indicating lower discharge efficiency.

However as temperature rises internal resistance reduces, so a continuous high current discharge may be more efficient than a pulsed discharge, even though the battery is running hotter! This is particularly noticeable at low ambient temperature.

Answer 3

Charge and discharge (and their efficiencies) are not the same thing, and you cannot use the same number for both. And internal resistance is mostly inapplicable to charging, but it's very useful for discharge.

In general, discharge efficiencies are greatest with the battery fully charged, while charging efficiency is least. And vice-versa.

Series resistance has two components. The first is the resistance of the electrode structure, which is usually (but not always) pretty negligible. What really counts is the electrolyte's ability to replace exhausted chemicals in the reaction zone with fresh, unexhausted ions. The limited mobility of ions in the solution puts a limit on how much current can be produced, although things like electrode structure also comes into play. So series resistance is actually something of an artificial construct, which (to some degree inappropriately) applies Ohm's Law to the current limits produced by the electrochemical processes. It's a very useful artificial construct, mind you, but it's not "fundamentally" accurate in the same way it is for a standard resistor. Among other things, an exact value for series resistance depends on current level, state of charge of the battery, and temperature.

When a battery is fully charged, all of the solution's ions are ready for use (sorry for the imprecise figure of speech) and it's easy to find replacement ions, so the series resistance is low. At very low charge levels, the series resistance goes up. Within limits, most batteries work better at the high end of their temperature range than at low.

For charging, the opposite effect occurs. With most of the electrolyte replenished, there aren't many ions floating around to accept the changes induced by the charge current, so more and more of the charge current is "wasted", and charge efficiency goes down. And generally, series resistance is not considered a useful concept when dealing with charging.