I voted for vini_i's answer, but there were two questions.
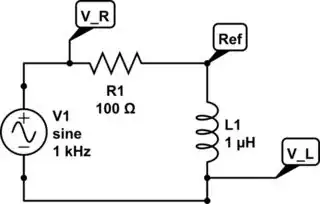
simulate this circuit – Schematic created using CircuitLab
Connect both grounds in-between components (or use one ground and leave the other disconnected) to serve as reference. Connect Channel 1 (or A) on resistor, 2 (or B) on inductor. Set \$ V_R \$ as trigger. Scope is measuring \$ V_R \$ vs \$ V_L \$.
Measure phase angle \$ \theta \$ on scope. It will be less than 90° because it is a non-ideal inductor. You may have to invert channel 2 (Pull Invert).
If it was an ideal inductor, the phase angle would be 90°. Real inductor is made of wire and wire has resistance \$ R_{DC} \$, plus a \$ R_{AC} \$ due to ac effects (hysteresis, eddy currents, skin effect, radiation), so phase angle will be less than 90°.
Measure \$ V_{R_{PP}} \$ on scope. Convert to RMS.
$$ V_{R_{RMS}} = \frac {V_{R_{PP}}} {2} \times 0.707 $$
Measure R. Use Ohm's Law to calculate current.
Measure \$ V_{L_{PP}} \$ on scope. Convert to RMS.
Calculate effective voltage using trig.
$$ V_{Eff} = V_L\ cos\ \theta $$
Calculate average power due to effective resistance in inductor.
$$ P_{Eff} = V_{Eff} \ I $$
Edit with reference to comment...
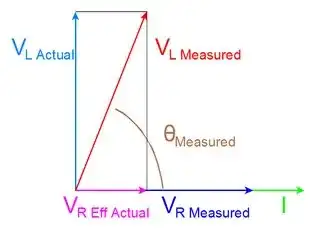
In the above circuit, you are looking into right triangle of the phasor diagram or \$ \theta_{Measured} \$ (Brown). You are measuring \$ V_{R_{Measured}} \$ (Blue) and \$ V_{L_{Measured}} \$ (Red). You cannot see the ideal inductor voltage \$ V_{L_{Actual}} \$ (Teal) or \$ V_{R_{Eff_{Actual}}} \$ (Purple). You cannot see I on the scope, but \$ V_R \$ is in phase with I, so seeing \$ V_R \$ effectively sees I.
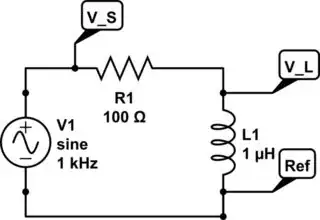
simulate this circuit
So if you connect it like so, scope is measuring \$ V_S \$ vs \$ V_L \$. You are seeing the angle at the top of the phasor diagram.
You could probably use sine instead of cosine, but I am NOT confident of that answer. By connecting it like my original answer or vini_i's, it will work.