12

The circuit looks like this: enter image description here

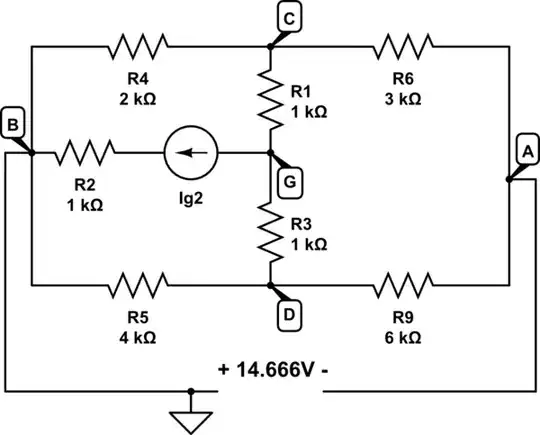
All the elements are known, except for \$I_{g2}\$.
\$E_1=3V,E_4=10V,E_6=2V,E_8=1V,E_9=4V,I_{g7}=1mA,\$
\$R_1=1k\Omega,R_2=1k\Omega,R_3=1k\Omega,R_4=2k\Omega,R_5=4k\Omega,R_6=3k\Omega,R_9=6k\Omega\$

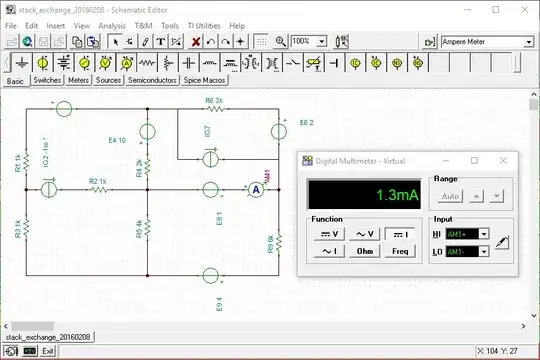
But we also know the current \$I_8=1.3mA.\$ The task is to calculate \$I_{g2}.\$
According to LTSpice software, \$I_{g2}=1mA\$.

What I did:
I transformed the whole circuit into Thevenin equivalent in regards to the branch with \$E_8\$. It was a long and demanding process, but, in the end, I got \$I_{g2}=11mA\$ which is nothing close to \$1mA\$.
I rechecked everything I did a couple of times, but I just couldn't find the mistake. I will recheck it a few more times, but I would like you to give me tips and your opinions on solving this, do you have any better ideas?

Edit:

So, here is the detailed procedure of my solution:
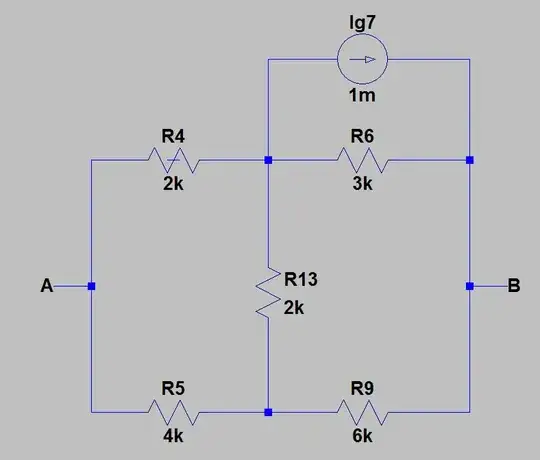
1) I redrew the circuit for easier calculations. The picture below shows the circuit for which I found the Thevenin's equivalent. enter image description here

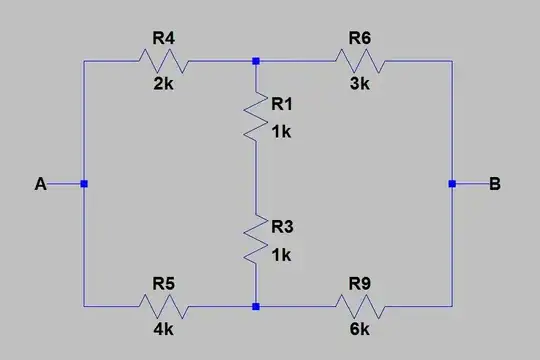
2) Then, I found the equivalent resistance between \$A\$ and \$B\$ by cancelling all the sources with their internal resistances. The picture below shows the circuit after the cancellation of sources. enter image description here

Now, I calculated equivalent resistance by replacing \$R_1\$ and \$R_3\$ with \$R_{13}=R_1+R_3=2k\Omega\$. Then I applied delta-wye transformation to convert \$R_4R_5R_{13}\$ into \$R_{45}R_{134}R_{135}\$. After that, everything is obvious.
After a few calculations I got: \$R_T=R_e=\frac{10}{3}\Omega\$.

3) For calculating the voltage between \$A\$ and \$B\$ I applied superposition theorem and taken in account one source by one.

  • a) only \$E_1\$ active: enter image description here

We can see the bridge is balanced, so \$E_1\$ has no impact on \$U_{AB}\$, so, in this case, \$U_{AB1}=0\$.

  • b) only \$E_4\$ active: enter image description here

Using node-voltage analysis, I found that, in this case, \$U_{AB2}=-\frac{20}{3}V\$.

  • c) only \$E_6\$ active: enter image description here

Again, using node-voltage analysis, \$U_{AB3}=-\frac{4}{3}V\$.

  • d) only \$E_9\$ active: enter image description here

Again, using the same method, we get \$U_{AB4}=-\frac{4}{3}V\$.

  • e) only \$I_{g7}\$ active: enter image description here

Using current dividers, I got: \$U_{AB5}=-2V\$.

  • f) only \$I_{g2}\$ active: enter image description here

This is the part where I lost so much time, I found this circuit really complicated, but, solved it in the end using the combination of delta-wye transformation of \$R_4R_5R_{69}\$, compensation theorem and node-voltage analysis. Then, from the circuit I got, I calculated currents through \$R_1\$ and \$R_3\$ and then I used compensation theorem (replaced resistor \$R_1\$ with voltage source \$E_1=\frac{51}{84}I_{g2}\$ and resistor \$R_2\$ with voltage source \$E_3=\frac{33}{84}I_{g2}\$). After this, I used node-voltage analysis and in the end got \$U_{AB6}=\frac{4}{3}I_{g2}\$.

Then, I summed up all the voltages and got \$E_T=\frac{4}{3}I_{g2}-\frac{34}{3}\$

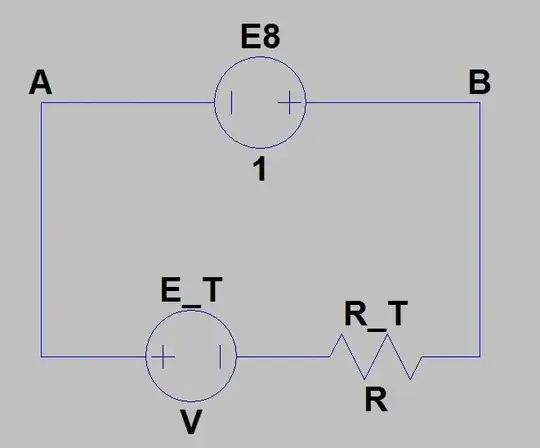
Now, finally, the equivalent circuit looks like this: enter image description here

And, since we know that the current through that circuit is \$I_8=1.3mA\$, we get \$I_{g2}=11mA\$, which is incorrect.
I hope you can find the mistake somewhere.

Thank you for your time.

A6SE
  • 379
  • 1
  • 8
  • 24
  • You ought to post your work. If we can't see your work, how will we know where you went wrong? – uint128_t Jan 25 '16 at 00:18
  • It takes around 7 pages in my notebook, I will post it in the edit section. – A6SE Jan 25 '16 at 00:24
  • @uint128_t I modified the question with detailed procedure. – A6SE Jan 25 '16 at 01:37
  • You should post your answer as an actual answer, so that the question can be closed (and I can upvote twice) – jms Feb 08 '16 at 12:53
  • Without bothering to find the precise issue, I'll say that it's nearly always a sign error, i.e. the fact that the direction of Ig7 is drawn going from negative to positive WRT the voltage sources, or that E4 and E6 are in opposition (around the loop) because they are the same way "up" but on opposite sides of that loop. That, and I prefer to give problems that are a bit less contrived... – Ecnerwal Feb 08 '16 at 13:57
  • Perhaps superposition is the way to go - e.g. there's a balanced bridge across E8. – Chu Feb 08 '16 at 15:14

3 Answers3

8

Found it! In your schematic for the \$E_4\$ Thevenin voltage, you drew \$E_4\$ backwards. The positive end should point towards the 2k resistor. This led to a sign error that caused you to miscalculate the \$I_{g7}\$ Thevenin voltage.

I figured this out while typing up the very long answer below. I'm leaving it here because A) I spent a lot of time on it, and B) someone might find it helpful to see the full process of figuring this out.

Mesh analysis seems like a much better choice for this than a Thevenin equivalent, but let's try it your way...

You never actually said what you think the Thevenin voltage is. We have \$E_8\$, \$I_8\$, and the Thevenin resistance, so that leaves one variable:

$$\frac {E_8 - V_T} {R_T} = I_8$$ $$\frac {1 \mathrm V - V_T} {3.333 \mathrm{k\Omega}} = 1.3 \mathrm{mA}$$ $$V_T = -3.333 \mathrm V$$

Using your formula:

$$V_T = \frac 4 3 I_{g2} − \frac {34} {3}$$

\$I_{g2}\$ comes out to 6 mA. I don't see how you got 11 mA out of that. Regardless, the problem has to be with your formula relating \$V_T\$ and \$I_{g2}\$. I simulated the Thevenin voltage for each source in CircuitLab and verified that your calculations are correct. That suggests your \$I_{g2}\$ calculations are wrong.

I think the easiest way to do proceed is to compute the Thevenin voltage of the \$I_{g2}\$ circuit first. I chose the right side of the \$E_8\$ branch as the positive one above, so I'll continue that here:

$$V_T = V_{T,I_{g2}} + V_{T,others}$$ $$-3.333 \mathrm V = V_{T, I_{g2}} + 11.333 \mathrm V$$ $$V_{T, I_{g2}} = -14.666 \mathrm V$$

Now let's try to solve for \$I_{g2}\$:

schematic

simulate this circuit – Schematic created using CircuitLab

Now we can do some nodal analysis:

$$\frac {-14.666 \mathrm V - V_C} {3 \mathrm k\Omega} + \frac {-14.666 \mathrm V - V_D} {6 \mathrm k\Omega} = 0$$

$$\frac {V_C} {2 \mathrm k\Omega} + \frac {V_C - V_G} {1 \mathrm k\Omega} + \frac {V_C - -14.666 \mathrm V} {3 \mathrm k\Omega} = 0$$

$$\frac {V_D} {4 \mathrm k\Omega} + \frac {V_D - V_G} {1 \mathrm k\Omega} + \frac {V_D - -14.666 \mathrm V} {6 \mathrm k\Omega} = 0$$

That gives \$V_C = -13.88 \mathrm V\$, \$V_D = -16.237 \mathrm V\$, and \$V_G = -20.559 \mathrm V\$. Now there's just one more KVL equation:

$$\frac {V_G - V_C} {1 \mathrm k\Omega} + \frac {V_G - V_D} {1 \mathrm k\Omega} = I_{g2}$$ $$\frac {-20.559 \mathrm V - -13.88 \mathrm V} {1000} + \frac {-20.559 \mathrm V - -16.237 \mathrm V} {1000} = I_{g2}$$

And that gives... 11 mA.

Huh.

I confirmed in simulation that 11 mA does give the right voltage for A - B (-14.666 V). But when I simulate the entire circuit, I confirm BartmanEH's result -- the correct answer is 1 mA. I took out \$E_8\$ and verified that the Thevenin voltage is -3.333 V, and connecting a 1 A test source, I verified that the Thevenin resistance is 3.333k. I re-ran the Thevenin voltages for each source with the full circuit and got:

$$V_{T,I_{g2}} = -1.333 \mathrm V$$ $$V_{T,E_1} = 0 \mathrm V$$ $$V_{T,E_4} = -6.666 \mathrm V$$ $$V_{T,E_6} = 1.333 \mathrm V$$ $$V_{T,E_9} = 1.333 \mathrm V$$ $$V_{T,I_{g7}} = 2 \mathrm V$$

Adding those up gives -3.333V, as expected.

A-ha! The \$E_4\$ Thevenin voltage is supposed to be the opposite sign from the rest. There's your error! Looking at your Thevenin voltage schematics, I see that \$E_4\$ is drawn backwards! Problem solved.

Adam Haun
  • 21,331
  • 4
  • 50
  • 91
  • Wow, thank you for your time, I really appreciate it. – A6SE Feb 09 '16 at 10:17
  • I have one confusion though, why is \$\frac{E_8-V_T}{R_T}=I_8\$? I thought is was \$\frac{E_8+V_T}{R_T}=I_8\$, according to my last picture. – A6SE Feb 09 '16 at 11:17
  • The polarity of \$V_T\$ is arbitrary. It just needs to be consistent. I find it more natural to think of the Thevenin voltage as opposing the source voltage, so that's what I did. The other way works too. – Adam Haun Feb 09 '16 at 14:17
  • The problem is, if I go my way, I get a wrong result (\$4mA\$), but if I go your way, the result is correct (\$-1mA\$). During the whole process, I calculated the voltage \$U_{AB}\$, not \$U_{BA}\$ and in the end, it equals: \$V_T=\frac{4}{3}\cdot10^3I_{g_2}-2\$. Then, if I go my way and use \$\frac{E_8+V_T}{R_T}=I_8\$, which is completely logical to me, I get the wrong result. – A6SE Feb 09 '16 at 15:05
  • 1
    If you change the polarity of a voltage, you need to negate its value as well. You missed the sign change somewhere -- the 2 should be positive, not negative. Your formula should be \$V_T = \frac 4 3 I_{g2} + 2\$. – Adam Haun Feb 09 '16 at 18:11
  • Yep, I made a mistake in summing the voltages in the end. It is \$+2\$, not \$-2\$. Thank you for your time. – A6SE Feb 09 '16 at 18:18
3

I whipped this up in TINA-TI free schematic editor/simulator: enter image description here I then iterated Ig2 until the Ammeter (I8) read 1.3mA and the result is that Ig2 is -1mA (negative 1 milliAmp) and not +1mA as you said LTspice produced. Looks like you entered Ig2 in reverse.

Either way, it looks like -1mA is the correct answer.

BartmanEH
  • 200
  • 1
  • 10
1

I don't think you can use that delta-wye conversion in that last circuit because of the branch in the middle of it. However, I tried solving only that circuit using mesh current equations and my final answer using your other values was still not 1 mA. I didn't work the whole problem though, so there may be other mistakes I didn't catch. I also could have done my calculations incorrectly.

JosephQ
  • 66
  • 6