5

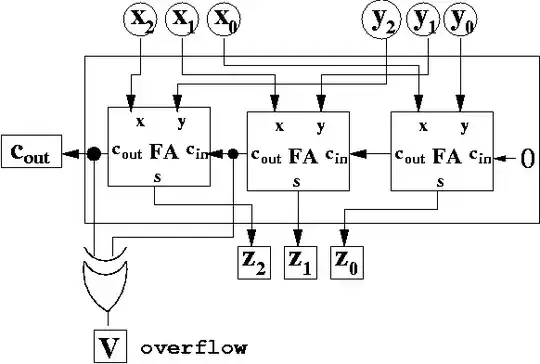
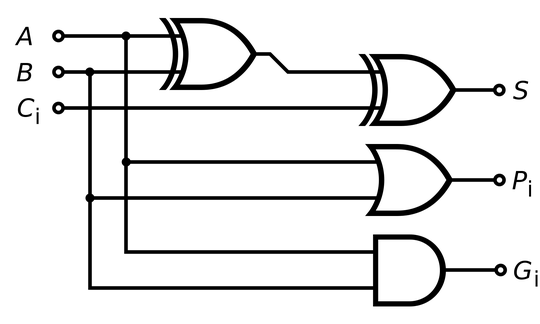
I am implementing a 32 bit CLA Adder like how a 16 bit adder is implemented in Wikipedia

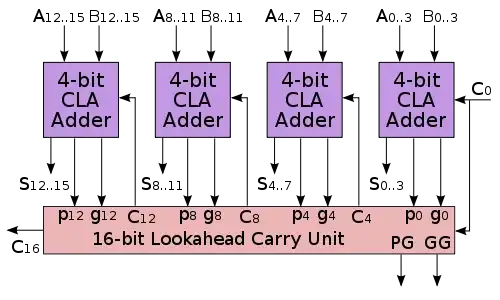
Problem is how do I determine if the block overflows? I will need the carry into bit 32 (which is now in the last 4 bit CLA Adder) and XOR with carry out of bit 32(Check difference in MSB)?

UPDATE

Is my overflow logic correct

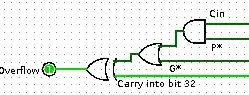
where Cin is the carry into the whole 16 bit block, P* is the Block Propagate, G* the block generate, and carry into bit 32 (typo, bit 16 MSB actually)

Community
  • 1
Jiew Meng
  • 569
  • 2
  • 12
  • 21

3 Answers3

1

I thought about seeing what my brain could regurgitate of long ago explnatins, as opposed to commin sense observations, BUT here's a page which does it all very well indeed.

They explain a "nice" 'trick'.

  • Two's compelment overflow detection can be achieved by XORing the carry-in and the carry-out bo=its of the leftmost full adder.

Their diagram. See above ref for detailed comment:

enter image description here

Russell McMahon
  • 147,325
  • 18
  • 210
  • 386
  • 2
    Thats a 1 bit adder, the problem with using a >1 bit adder is that the carry into the MSB is hidden somewhere in the adder itself. Hope you got me? I could have an output for my block adder for Cin to MSB but that seems off place? Alternatively, I could have evey block output an Overflow bit, is this the usual implementation? It will give quite abit redundant logic – Jiew Meng Oct 23 '11 at 13:22
  • The last stage output is the XOR of the two inputs and the carry in; thus the carry in is the xor of the two inputs and the output. – supercat Sep 15 '15 at 16:46
1

If you are designing the CLA (carry lookahead adder) block, you could have the block output the carry from the bit 2 digit (which must already be calculated in order to form the correct value for bit 3 of the sum).

If the CLA block interface is a given, you can derive overflow from the sign bits of the two adder inputs, A(31) and B(31), and the sign bit of the output sum. If A and B are the same sign, the sum sign must match them iff there is no overflow. For more detail, see this page or this page.

mgkrebbs
  • 538
  • 7
  • 11
1

You can retrace C(n-1) from P, G and S

If you use: X = XOR( P, G)

or you can also use XOR( !P, !G); P=Propagate, G=Generate

Ci(n-1) = XOR( X, S) ; S = sum result of highest bit

Now you have Ci(n-1) and Ci(n)

V = XOR ( Ci(n-1), Ci(n) ) ; see other theories above

G= P= X= Ci= Ci
AxB =Y xCi =S A&B A+B GxP XxS check
00 0 0 0 0 0 0 0 ok
11 0 1 1 1 1 0 1 ok
01 1 0 1 0 1 1 0 ok
10 1 1 0 0 1 1 1 ok

x = XOR; + = OR; & = AND; ! = NOT enter image description here

Paul
  • 11
  • 2