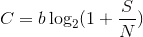Yes, Doppler will, on many systems, influence throughput.
First of all, though, as mentioned by the other answers, the induced symbol rate change will, on any system that I know, not be measurable. Point is that receivers always have to do some kind of timing recovery, if they try to achieve high throughput for a significant amount of time. That timing recovery will need to be there because no two oscillators are physically the same, so the transmitter's symbol clock will never be exactly the symbol clock a receiver would have generated by itself. As oscillator errors typically are in the parts per million down to parts per billion, if an extremely good oscillator was used, your doppler shift induced rate change will just be compensated by that. So yes, there's a rate change, but no, that won't be spottable at these speeds.
Then, of course, a transceiver is typically a complex system. Often, if not usually, if bidirectional, there's a method to ask for data that hasn't reached its target to be re-sent. If Doppler shifts your TX signal out of the "sweet spot" your receiver is currently tuned to, there's a good chance that will reduce SNR, and hence increase Symbol Error Rate, and hence increase packet error rate, and if forward error correction can't deal with that, throughput will be reduced by the amount of packets that have to be re-sent.
Many systems, amongst these WiFi, LTE etc. are rate-adaptive, in that they can reduce the modulation order, making the transmission more robust against error, and/or increase coding redundance, making errors easier to detect and correct. Both measures might kick in when Doppler stresses whatever control loop structure is used to track the signal, actively reducing the rate available. Keep in mind, however, that these systems typically optimize the rate:
Though Doppler doesn't introduce "new" noise, it can decrease SNR by reducing the signal power actually available for demodulation, or increasing the average error. For example, a frequency offset in a quadrature demodulation receiver will lead to a ongoing rotation of the constellation diagram. Hence, you will get something that looks like it was noise all the time -- your average received constellation point isn't on the spot it "should be" any more, but is most of the time off by a certain amount of degrees. That means that with less noise, you can make a symbol be misinterpreted as a neighboring symbol.
Reduced SNR will directly reduce the channel capacity:
Shannon's channel capacity is
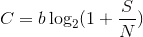
with b being the bandwidth, and S/N being the ratio of signal to noise power, all in bit/s.
No matter how good your modulation, how efficient your forward error correction is, you will never be able to transmit more bits per second over a channel than given by above formula.
Hence, the central trick one has to pull is making sure you can get as much of S out of your signal, and reducing N as far as possible. As mentioned above, a frequency shift looks like increased N, but if you have a control loop that corrects that fast enough, you can get low N, nevertheless.