The circuit below contains an AC current source and an ideal transformer along with some passive elements. I marked the points A and B, because I'm trying to find the power dissipated in the terminal A-B.
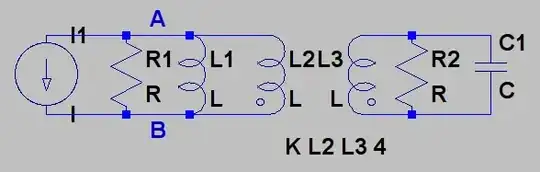
I could rewrite the circuit using Thévenin's theorem to this kind of circuit, where Z are complex impedances and V is a voltage source, because I feel safer calculating the power dissipation from this kind of source.
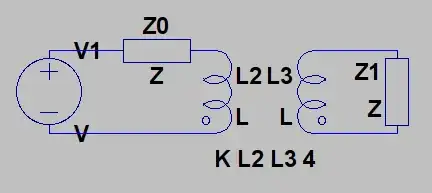
The part of the transformer on the left-hand side could be written as an impedance related to Z1 through \$(N_1/N_0)^2\$
Now, though, my question is: Which power dissipation in this "equivalent" circuit would be equal to the power dissipation over the A-B terminal above?