Compute the minimum number of 120Ω resistors to get 80Ω of resistance?

Question

I recently had to take test in basic electronics. I didn't get one question right, but I don't quite understand why.

How many 120Ω resistors are at minimum required to get a resistance of 80Ω?

The possible answers to this question are 2, 3, 4 and 6. The only answer I can come up with is 6, with the resistors arranged as seen bellow. But 6 isn't the correct answer.

Question:

How many resistors are required and to arrange them?

^{simulate this circuit – Schematic created using CircuitLab}

I only know the very basics of electronics, so I hope my thoughts are correct.

Answer 1

A direct solution can be found through the application of continued fractions.

If what you have is 120Ω and what you want is 80Ω, write down the fraction:

$$\frac{80\Omega}{120\Omega} = 0.6667$$

Since the integer part is zero, you'll be starting by putting resistors in parallel. Invert the fractional part:

$$\frac{1}{0.6667} = 1.5$$

This tells you that you'll have 1 resistor in parallel with some number of resistors in series. Invert the fractional part again:

$$\frac{1}{0.5} = 2.0$$

This tells you that you need 2 resistors in series. Since there is no fractional part at this point, you're done.

The answer is a total of 3 resistors.

Answer 2

120 || (120 + 120) If two 120 in parallel give 60, you want one of the branches to be a little higher, so... that's the next thing to try.

---

And the method is true in general for getting a 2/3-valued resistor using just a bin of the same kind. And in general for solving problems like this, it's worth remember that the equivalent resistance of two parallel resistors is less than that of either of the branches. You can also get 3/4 (so 90) for example by adding one more to a branch.

N.B.: Thanks to Massimo Ortolano's paper, now I know that what I've done above following just intuition is that I basically followed the search path indicated below in the Stern–Brocot tree:

Answer 3

You can change your solution by swapping serial and parallel:

^{simulate this circuit – Schematic created using CircuitLab}

You can then group R2, R3, R5 and R6 into a single 2x2 group:

^{simulate this circuit}

And those 4 \$120\Omega\$ resistors make a single \$120\Omega\$ resistor:

^{simulate this circuit}

Answer 4

Take your solution but without a central point in the middle: you can rearrange this as three parallel sections of 120+120 Ohm each (connecting the middle points does not make a difference since they all are at the same voltage). Now two of the three parallel 120+120 Ohm sections combine into 120 Ohm again, so you can replace those 4 resistors from the two parallel groupings with a single one, leaving just one 120 Ohm resistor parallel to 120+120 Ohm.

There is a plethora of solutions proving the correctness of this solution once you have it. But this rearrangement shows how to find it without reverting to mathematical trial and error.

Answer 5

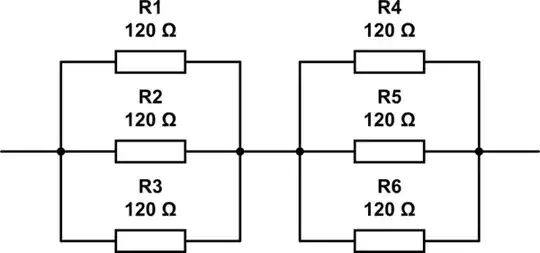
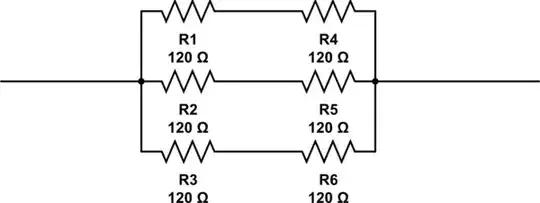
Elaborating on @RespawnedFluff's answer, one way to find this is to think in the following way:

1. What resistors do I have, ok 120.
2. What do I need to make, 80
3. What equations do we know? Well the two resistors in series or parallel are the simplest starting points. Clearly series doesn't help immediately - that would increase the resistance, not reduce it. So we will need to try parallel. We know the equations:

$$\frac{1}{R_p}=\frac{1}{R_1}+\frac{1}{R_2}=\frac{R_1 + R_2}{R_1 R_2}$$

4. So maybe lets start with that:

$$\begin{align} \frac{R_1 R_2}{R_1 + R_2} &= 80\\\\ 80R_1 + 80R_2 &= R_1 R_2\\\\ R_2 &= \frac{80R_1}{R_1-80} \end{align}$$

5. So can you find any combination that suits? Well, start with \$R_1=120\$ and then see what value \$R_2\$ needs to be. Can you make that value easily? In this case yes, so great.

6. For other values, if you can't get a value immediately, you may need to try either the same approach as above iteratively to find the value for \$R_2\$. If that fails to work, you could also try changing \$R_1\$ - maybe two in series or parallel, and then try again for \$R_2\$.

This approach is quite iterative, but in this case it would have quickly found both the answer you got (using 6 resistors), and also the answer @RespawnedFluff got (using 3 resistors).

If you were trying to grow the resistance (i.e. the required resistance is larger than your available value), you basically do the same thing, but start with a larger available resistance, or split the larger resistance up in series chunks and solve for them (e.g. if you wanted \$180\Omega\$, you could pick a chunk of \$120\Omega\$ and \$60\Omega\$).

---

You may wonder how the method would have gotten to your answer - given that yours has 3 parallel branches, whereas this approach uses two. Well, in calculating \$R_2\$ above, iteratively, you would introduce \$R_2\$ being a parallel branch, which topologically is the same as if there were 3 branches to begin with.

Answer 6

Basic resistance in series and resistance in parallel logic. Very simple..

We know the output is 80Ω, so solving the problmm is easy. Try the formula for parallel resistance: $$\frac{1}{Rp} = \frac{R1+R2}{R1\cdot R2}$$ Therefore.. $$Rp = \frac{R1\cdot R2}{R1+R2}$$ Here put \$Rp = 80\Omega\$.

Now as we know we have resistors of only 120Ω. Put \$R1 = 120\Omega\$

Solving ... you will get \$R2 = 240\Omega\$.

But we cannot use a 240Ω resistor here as it's said that we have only 120Ω resistors. So instead of 240Ω, we will use 120Ω + 120Ω (in series) in parallel with a single 120Ω resistor.