This seems to be a homework or self-educational question, so I won't show the full solution. Just three starting points.
There's no physical reason to mirror the charge, but I quess it makes calculation easier and / or less error-prone. Don't forget to mirror the solution and reassemble the two line charges again at the end!
Integrating over x
The simplest approach to calculate the field at point M is to use the formula for the field of a point charge and integrate it over the total charge.
Let's introduce a new parameter \$b\$ which should denote the distance between a certain portion \$dQ\$ of the charge distribution to the origin \$O\$. This means \$b\in[0;a]\$, and you can rewrite \$dQ=\rho_s\,db\$.
Now, the field generated by a piece \$dQ\$ of charge is:
$$d\vec{E}=\frac{dQ}{4\pi\varepsilon_0}\frac{1}{|r|^2}\frac{\vec{r}}{|r|}=\frac{\rho_s}{4\pi\varepsilon_0}\frac{\vec{r}}{|r|^3}\,db$$
$$\vec{E}=\int_0^a\frac{\rho_s}{4\pi\varepsilon_0}\frac{\vec{r}}{|r|^3}\,db$$
The problem here is that
$$\vec{r}=\begin{pmatrix}x+b\\y\end{pmatrix} \ \Rightarrow \ |r|^3=\sqrt{(x+b)^2+y^2}^3$$
which makes the integration a bit tough.
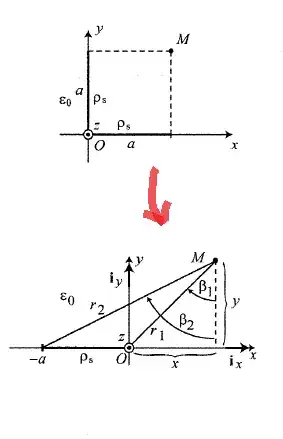
Integrating over \$\beta\$
The second sketch implies that you may integrate over an angle \$\beta\$. Note you can write
$$\vec{r}=\underbrace{\begin{pmatrix}\sin\beta\\\cos\beta\end{pmatrix}}_{=\vec{r}/|\vec{r}|}\cdot\frac{y}{\cos\beta}=\begin{pmatrix}y\cdot\tan\beta\\y\end{pmatrix}$$
which simplifies your integral. Note that the integration interval now is \$\int_{\beta_1}^{\beta_2}...d\beta\$. Also, you have to find a new expression \$dQ=...d\beta\$. (I didn't calculate this and also didn't try out how difficult the integral becomes)
Different approach using potential
Another standard approach is to calculate the potential via
$$\vec{V}=\int_0^a\frac{\rho_s}{4\pi\varepsilon_0}\frac{1}{|r|}\,db$$
which is much simpler. The E-field can then be calculated via \$\vec{E}=\vec{\nabla}V\$.
To my knowledge, this is the standard way to calculate the field of a line charge.