The potentiometer on the left of the circuit below is actually the output of a digital potentiometer designed for audio volume control, so its outputs are internally configured to offer 64 logarithmic steps, from 0dB to -64db. I can't change that. Now as it turns out, I need to use the output to control an audio amplifier that has an internal DSP processor, which accepts 0-3.2VDC to control its audio volume. That amplifier currently gets that voltage from a linear potentiometer, so it is internally doing its own linear to log conversion. So using the circuit shown without the diodes, with just R11 and R12 used as a simple voltage divider to convert my 0-12V to a 3.2V range, it works but the response is less than ideal. Since the output of my digital pot is advancing the voltage in 1 dB steps, the "steps" become audibly noticeable in that amplifier's output level, especially as the higher volumes are reached. So what I need to do is convert the logarithmic steps to some approximation of linear, meaning I need an anti-log function.
So I'm thinking of approximating an anti-log curve with a couple of diode networks as shown. Basically, the output voltage will initially follow the input voltage, but then rise progressively slower as D2, and then later the D3-D4 pair begin to conduct. It seems to work well enough to make the volume control sound more responsive, but somehow the circuit just seems to be a "hack" to me. Can anyone suggest a more eloquent solution that doesn't involve a huge amount of additional parts? 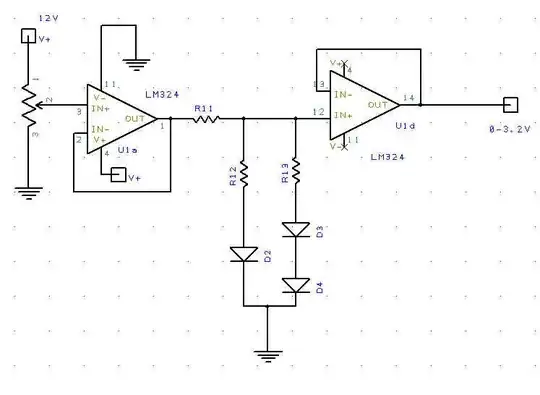
Addendum... After playing trial and error with the above circuit all day, feeding it with a linear ramp and comparing input to output, I decided it was too difficult to optimize. Should the max reference voltage (12 V in the above) change at all, too many resistors have to change to duplicate the desired response. But on a whim I came up with this. I honestly have no idea if I'm really approximating an anti log (or log) response with this configuration, but I found it very easy to "tune" to a desired response, as long as the max input reference voltage was at least 2 or 3X the desired final output max. The gist is, as the input POT was adjusted higher, the output would gradually diverge from the input, so that input changes had progressively less affect on the output. The final test of course was to actual try it with an audio signal through the voltage controlled amplifier, and I thankfully found the digital POT control to be much more natural.
I'd still welcome comments on why this seems to be working so well, whether I am indeed approximating the non inverting log curve I'm after, and whether it could be done simpler. But bottom line, if anyone else runs into a similar problem, this does seem to work VERY nicely... at least to my ears!
Another addendum: For the benefit of anyone following this in need of a similar circuit, I need to point out the the LM324, despite being a common choice for single supply OP-AMP circuits, turned out to be a poor choice for this otherwise good circuit. The reason being, this OP amp is based on internal BJT transistors, and so it really can't "drive" any output below 0.6 volts. In my case, even though I didn't need the LOG response curve to start below that point, the circuit still needed to output 0-3 volts into an existing circuit that had a small positive bias current, and so I was not able to adjust the output down to zero, even if I grounded the final OP amp used as a buffer). So I will likely replace the quad OP amp with something like the Texas Instruments TLC274, because being FET based, its output Voltage Range actually does Include the Negative Rail