So if I want my LC circuit to resonate at 20MHz, I just use the formula, \$F=\frac{1} {2\pi\sqrt{LC}}\$. Using available inductor and capacitor values, there are lots of different possible combinations. If L is small, C is big or vice-versa. Or they could be about equal.
Will it make any difference at all in the actual operation of the circuit?
Will one way be less efficient and decay faster?
Many values of L and C produce the correct centre-frequency but, an important consideration is how tight the bandwidth is. Increasing "Q" (proportional to \$\sqrt{\frac{L}{C}}\$) makes the bandwidth tighter: -
And this is one of several ways of defining Q: -
Q = \$\dfrac{f_0}{f_2 -f_1}\$
The type of circuit modeled in many filters and oscillators consists of a parallel C with an inductor (L) of finite series resistance (losses): -
Usually the inductor copper and hysteresis losses far outweigh dielectric losses of the tuning capacitor so this model is preferred rather than one that has a resistor in parallel with C. Normally, the natural resonant frequency is defined as \$\frac{1}{2\pi\sqrt{LC}}\$ but because of R, the oscillator frequency is slightly different at: -
Because the three components can also be seen to be in series, the Q factor of the circuit is also: -
The upshot of all of this is that Q can be increased by raising L whilst reducing C but, there gets a point when the self resonant frequency of the inductor is reached and nothing further can be done.
For more info check out the wiki page here
I'm being harassed into proving that if you doubled the turns on the inductor there is a net benefit to Q increasing. Consider that doubling the turns also doubles the resistance and this is bad for Q. But doubling the turns will also quadruple the inductance and, to keep the same operating frequency C has to quarter. Therefore the ratio of L/C becomes 16*L/C and so taking the square root the new value of Q becomes \$\frac{1}{2R}4\sqrt{\frac{L}{C}}\$ or Q doubles.
Although the circuit resonates at the same frequency as long as the product of L and C is the same, the impedance changes. The impedance is given by the sqrt(L/C) ratio.
This may not mean much when you're just playing around with resonance, and getting the frequency right. However, it becomes important when designing filters and oscillators.
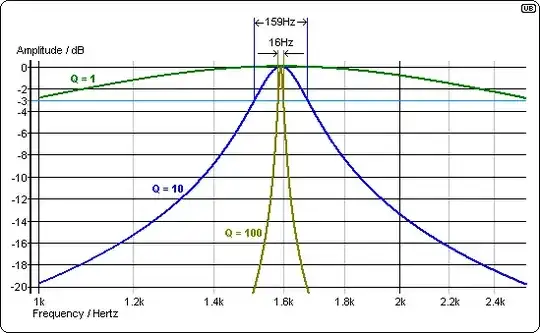
Once you have loss in a circuit, you need to consider the circuit Q, also known as quality factor. This controls the bandwidth of the resonance. For a series resonant circuit, is given by L/R. For a constant loss term, changing the L/C ratio will change the circuit Q. If you use a filter design program, you won't have to worry about this too much, as when you specify a filter shape, and a terminating impedance, the program gives you the correct component values. If you change the component values, even keeping the product constant, the filter shape will change, due to changing the loaded Q of the elements, given the fixed termination resistance.
When you are playing with a simulation, or answering college questions, you will often vary the R terms to vary the Q. However, in real life, you sometimes don't have the opportunity to alter R. You may want a filter to work in a 50\$\Omega\$ system, your varactor may have an irreducible 1\$\Omega\$ series resistance, your bipolar oscillator transistor a very low and unincreasable effective base resistance. Then you have to worry about LC ratio.
Low noise oscillator designs that I have seen happening on the next bench along (I'm not an oscillator designer) have used 8 varactors in parallel and 10mm of 3mm wide track for the inductor at 500MHz. Not many people realise how important the L/C ratio is, which is why there are so few good oscillator designers, or really good oscillators.
TeX does work BTW, but I did have to dig around a bit to find out how. On this site, escape the $ with a \
In theory, with ideal components, there would be no difference. In practice you will probably find that for a given inductor size coil resistance will increase significantly and may affect Q. On the other hand when using too small a capacitor you may find PCB capacitance affects the circuit.
There's no theoretical difference between increasing C and decreasing L (or vice-versa). The practical difference comes in figuring out how to buy/build those actual components.
In my experience, it's usually easier to increase C than L (especially if your circuit is going to be high-current). High-valued inductors generally need a lot of turns of wire, which means they tend to be physically larger and/or have higher DC resistances.
If you can, try to stay to stable ceramic capacitors. So that's NP0/C0G, X7R, or X5R. The more precise, the better. Also try to oversize their voltage rating by a factor or 2 or more.
For picking components in an LC circuit, I'd say my general process goes something like this:
If I don't want to design my own inductor:
If I do want to design my own inductor:
In an oscillating LC circuit energy is swapped continuouly between an inductor and a capacitor, i.e. at one moment when current is at maximum the inductor contains all the energy (\$E_L=\frac{1}{2}LI^2\$) and after \$\frac{1}{2}\$period, when voltage is at maximum the capacitor contains the same amount of energy \$E_C=\frac{1}{2}CV^2\$).
As you've pointed out you can have the same resonance frequency with different combinations of L and C, but what differs is the ratio between (max. or average) current and voltage. That ratio is not unimportant for at least two reasons:
A real LC circuit always is actually a RLC circuit, i.e. there are some resistances involved. Probably most relevant are series resistances of the inductor (and maybe also of the capacitor).
In order to minimize losses in series resistances it is better to have low currents and high voltages, i.e. high inductance and low capacitance.
Example: If you compare the LC combinations \$L_1\$=100µH, \$C_1\$=1nF and \$L_2\$=1µH, \$C_2\$=100nF currents will be 10 times higher in the second combination (this assumes that series resistance is the same in both cases; in reality the higher inductance probably will have also a higher series resitance).
If parallel resistances are dominant, in order to minimize losses it'd be better to have high currents and low voltages, i.e. low inductance and high capacitance.
Another requirement for the ratio between voltage and current, called impedance, is given by the surrounding circuit that requires it to be in a certain range. It must match the connected circuit (e.g. an amplifier) in order to have efficient energy transfer.
So, in theory you may choose L and C arbitrarily. But in practice it depends on what you want your LC-Circuit for. From time to time, I'm just messing around with some passive elements (R,L,C) in the RF range. A very practical problem is that when the capacitance is very small the measuring device already has a huge impact and thus changes the center/resonance frequency of your circuit. When measuring with an oscilloscop you add a capacitance of order ~pF so you have to consider this. On the other hand, often you have to make inductors yourself when you want a certain inductance. Of course, you can just wind some copper wire to a coil but in practice, making a good/matching inductor was one of the most difficult and time consuming things I did. Additionally, measuring the coil isn't very easy without advanced equipment. (Fortunately, I could mess around with a VNA)
Once you find good THEORETICAL values for L and C, that resonate at a desired frequency, (for example, a 7.03619mf cap and a 1mh coil can be used as a 60Hz hum filter), then you can find the most EFFICIENT L-C values, by finding where their slopes intersect!
Simply multiply L times C, and take the square root of the answer. Above, this would be SQRT(0.00703619 x 0.001) = 0.002652582.
So, a fabulous 60Hz filter would have the values C=2.653mF and L=2.653mH. Keep the actual values near this point, and you'll be singing the HAPPY song, with no line hum through the speakers!
