Finding the cut-off frequency

Question

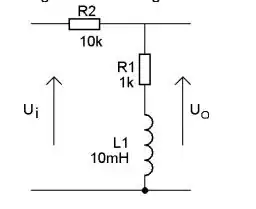
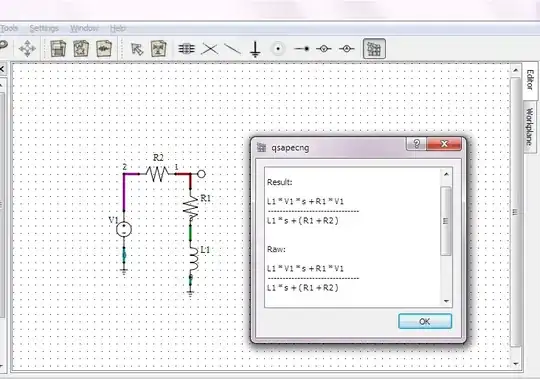
Find the cut-off frequency of this filter:

My attempt:

$$\text{H}\space_{\left(\omega\right)}=\frac{\text{R}_1+j\omega\text{L}}{\text{R}_1+\text{R}_2+j\omega\text{L}}=\frac{\text{R}_1+j\omega\text{L}}{\text{R}_1+\text{R}_2+j\omega\text{L}}\cdot\frac{\text{R}_1+\text{R}_2-j\omega\text{L}}{\text{R}_1+\text{R}_2-j\omega\text{L}}=$$ $$\frac{\text{R}_1^2+\text{R}_1\text{R}_2+\left(\omega\text{L}\right)^2+j\omega\text{L}\text{R}_2}{\left(\text{R}_1+\text{R}_2\right)^2+\left(\omega\text{L}\right)^2}$$

So when you're looking for the cut-off frequency you can say:

$$\Re\left(\text{H}\space_{\left(\omega\right)}\right)=\Im\left(\text{H}\space_{\left(\omega\right)}\right)$$

So we get:

$$\text{R}_1^2+\text{R}_1\text{R}_2+\left(\omega\text{L}\right)^2=\omega\text{L}\text{R}_2\Longleftrightarrow$$ $$\left(\omega\text{L}\right)^2-\omega\text{L}\text{R}_2+\text{R}_1^2+\text{R}_1\text{R}_2=0\Longleftrightarrow$$ $$\omega^2\text{L}^2-\omega\text{L}\text{R}_2+\text{R}_1^2+\text{R}_1\text{R}_2=0\Longleftrightarrow$$ $$\omega=\frac{\text{L}\text{R}_2\pm\sqrt{\left(-\text{L}\text{R}_2\right)^2-4\cdot \text{L}^2\cdot \left(\text{R}_1^2+\text{R}_1\text{R}_2\right)}}{2\cdot \text{L}^2}\Longleftrightarrow$$ $$\omega=\frac{\text{L}\text{R}_2\pm\sqrt{\left(\text{L}\text{R}_2\right)^2-4\cdot \text{L}^2\cdot \left(\text{R}_1^2+\text{R}_1\text{R}_2\right)}}{2\cdot \text{L}^2}$$

Am I doing something wrong?

Answer 1

The transfer function is (obviously):

$$ H(s) = \frac{R_1 + L_1s}{(R_1+R_2)+L_1s}$$

The point of doing that was to plot

Adopting def of cut-off frequency as that of a high-pass filter, the eyeometer (or a numerical solver) will give us the -3dB roll-off around \$10^6\$ rad/s.

To calculate this symbolically just calculate the square of the gain (since \$G(j\omega) = |H(j\omega)|\$) as

$$(G(j\omega))^2 = H(j\omega)\overline{H(j\omega)} = \frac{R_1 + L_1j\omega}{(R_1+R_2) + L_1j\omega} \frac{R_1 - L_1j\omega}{(R_1+R_2) - L_1j\omega} = \\ = \frac{R_1^2 + (L\omega)^2}{(R_1+R_2)^2 + (L\omega)^2} $$

(Don't try to do the above in Wolfram Alpha as unlike Mathematica you can't tell it to assume those parameters are real, so it will give you some unsimplified complex number result.)

Now solve \$(G(j\omega))^2 = \frac{1}{2}\$ for \$\omega\$ positive, to get

$$ \omega = \frac{\sqrt{-R_1^2+2 R_1 R_2+R_2^2}}{L_1} = \frac{R_2}{L_1} \sqrt {2-\Big(\frac{R_1}{R_2}-1\Big)^2} $$

This is certainly sensible (positive real) when \$R_2>R_1\$ (or more precisely when \$R_2 > (\sqrt{2} - 1) R_1\ \approx 0.41 R_1\$). If this doesn't hold (e.g. large \$R_1\$ say 100K in this example), then the gain doesn't ever drop below -3dB. Also note that for a simple high-pass RL filter you'd only have the \$ \frac{R_2}{L_1} \$ part, which you can obtain as particular case by making \$R_1 = 0\$.

If you substitute the numerical values from your problem into this, you get basically the same result as via the graph/eyeometer: \$1.09087×10^6\$ rad/s (i.e. 175.3kHz).