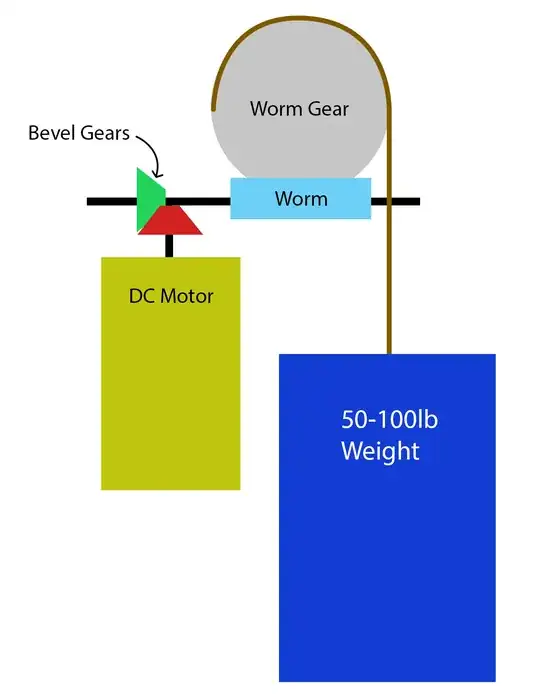
If it doesn't matter how fast the weight is raised, then any size motor will do.
The reason?
Lifting a certain weight requires tension in the cable, torque through the rest of the geartrain, and current in the motor.
Lifting at a certain speed requires m/s at the cable, radians/s through the geartrain, and voltage at the motor.
Lifting the weight at a certain speed requires power from end to end, always measured in watts. At the output, the power to lift the weight is speed*force in m/s and N. Through the geartrain the power is angular speed * torque, in radians/s and Nm. At the motor, the power is volts * amps. Losses in the geartrain and motor reduce the power available at the output, at best 50% through the motor and another 50% through the worm gear.
The ratios between torque, speed, force, current, voltage etc are determined by your gear sizes, gear ratios, motor voltage constants etc. The power is always power, no matter what the gear configuration and the motor type.
To put real numbers on it, start by putting your units into SI, appropriate for physics. A 100lb weight is about 50kg, is about 500N. If you want to lift that at 1m/s, you will need 500 W, or maybe 2kW electrical input. Not possible in your 50mm dia motor. If you want to lift at 1mm/s, you will need 0.5W, perhaps 2W electrical input. Much more possible.
Once you have a power budget, you look at a gear catalogue to see what ratios are available. Then convert forces through the gearing to get torque and speed at the motor. Then look at a motor catalogue to find a motor that will deliver those. Iterate gear choice as required. Rinse and repeat.
/edit/ Thanks to respawnedfluff for pointing out the static friction aspect. Any bearing will have a static, or 'breakaway', friction that is larger than its running friction. For a wormgear, that's true in spades. Do all the sums for dynamic operation. Then make sure your motor and power supply can deliver 2 to 3 times the operating torque, transiently, at the start to get things moving. Most DC PM motors will be able to do this, as will most batteries, and simple power supplies. A current-limited supply will have to be adequate for the starting torque however, not just the running torque.
Aristotle, or was it Archimedes, said 'give me a lever long enough and I will move the world'. Similarly, give me a worm gear with a large enough gear ratio, and I can shift a large weight with a tiny motor, albeit very slowly.
It is a very specialised worm gear that will run backwards, low ratio, nice materials, properly lubricated. For 'most' worm gears, their efficiency is so low that they cannot be backdriven by the load. The OP is correct that the worm will hold the load with the motor undriven. /edit/
As in most things in life, I find it's easier to do an analysis of a straw-man system, and then tweak that, rather than a synthesis from specifications. So... let's say you can get a 150:1 worm drive, and a 10 watt 3000 rpm motor, and ignore mechanical losses initially. 3krpm is about 300 rad/s, so the motor torque is 10/300 = 0.033Nm. After 150:1 gearing, we have 5Nm at the worm. To lift 500N, we need to wind the cable around an axle of radius 0.01m. 3krpm /150 = 20 rpm at the worm, 1 rev in 3 seconds, or 20mm/second.
Allowing for worm efficiency < 50%, we need to increase motor power, and to allow for starting torque, increase the power supply transient current above that. Is 20 watt motor and 20mm per second adequate?
If not, figure out where the biggest wrong assumption is, and rework.
You have drawn a 1:1 bevel. You have the opportunity to reduce motor speed and increase torque by using an N:1 bevel. Look at your gear catalogue for available ratios.