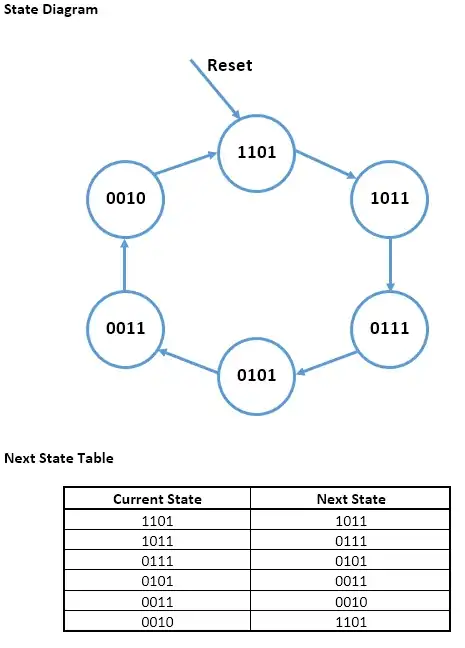
I have recently began studying Digital Electronics and have hit a wall trying to figure out how to design FSMs. At the moment, I am attempting to desing the FSM in the title which generates the following states: 1101->1011->0111->0101->0011->0010. Am I right in saying that this is a Moore machine and there will be 4 DFFs in this circuit? And what are the inputs for the circuit?
I now need to create the Karnaugh maps and this is where I am really stuck. I understand K maps and can create them, but I don't understand how you determine how many K maps are needed, and what goes in the x-axis and y-axis of the K maps when designing an FSM?
Here is what I have come up with so far:
EDIT
3rd bit Karnaugh Map: